题目内容
设f(x)=ax2+bx+c(a≠0),如果对任意x∈[-1,1],都有|f(x)|≤1,则对任意x∈[-1,1],均有|2ax+b|≤4.
证明:设g(x)=2ax+b,则g(x)为单调函数.故只需证|g(1)|≤4,且|g(-1)|≤4.
由于对任意x∈[-1,1],均有-1≤f(x)≤1.
∴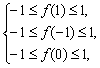 即
即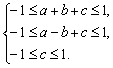
∴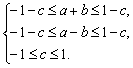 ∴
∴![]() ∴-2≤a≤2.
∴-2≤a≤2.
又∵
∴-4≤g(±1)≤4,即|g(±1)|≤4.
∴对任意x∈[-1,1],均有|2ax+b|≤4.
点评:构造一个函数,使要求证的不等式的左右两边是这个函数在某个单调区间上的两个值,则我们就可以利用函数的单调性证明不等式.

练习册系列答案
相关题目