题目内容
设f(x)=ax2+c,且-3≤f(1)≤1,-2≤f(2)≤3,求f(3)的最大值与最小值.
思路解析:此类问题应由f(1)、f(2)整体代入,否则单独求9a或c的范围,易导致范围扩大. 解法一:∵f(x)=ax2+c,∴ 解得 ∵-2≤f(2)≤3,∴- 又∵-3≤f(1)≤1,∴- ①+②,得- ∴f(3)的最大值是13,最小值是-7. 解法二:由已知f(1)=a+c,f(2)=4a+c,f(3)=9a+c, 设存在实数m,n使9a+c=m(a+c)+n(4a+c), 即9a+c=(m+4n)a+(m+n)c. ∴ ∴- 上两式相加,得-7≤9a+c≤13,即-7≤f(3)≤13. 故f(3)的最大值是13,最小值是-7.
![]()
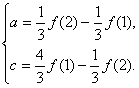 ∴f(3)=9a+c=
∴f(3)=9a+c=![]() f(2)-
f(2)-![]() f(1).
f(1).![]() ≤
≤![]() f(2)≤8.①
f(2)≤8.①![]() ≤-
≤-![]() f(1)≤5.②
f(1)≤5.②![]() -
-![]() ≤
≤![]() f(2)-
f(2)-![]() f(1)≤8+5,即-7≤f(3)≤13.
f(1)≤8+5,即-7≤f(3)≤13.![]() 解得
解得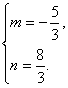
![]() ≤-
≤-![]() (a+c)≤5,-
(a+c)≤5,-![]() ≤
≤![]() (4a+c)≤8.
(4a+c)≤8. 练习册系列答案
练习册系列答案
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
相关题目