题目内容
设平面 与平面
与平面 相交于直线
相交于直线 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:若 ,又因为平面
,又因为平面 与平面
与平面 相交于直线
相交于直线 ,直线
,直线 在平面
在平面 内,且
内,且 ,所以由面面垂直的性质定理得:
,所以由面面垂直的性质定理得: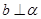 ,又因为直线
,又因为直线 在平面
在平面 内,所以
内,所以 ;
;
若 ,则得不到
,则得不到 ,假若给出直线
,假若给出直线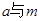 相交的条件,就可以得到了。
相交的条件,就可以得到了。
考点:面面垂直的性质定理;面面垂直的判定定理。
点评:本题主要考查对面面垂直的性质定理和面面垂直的判定定理的理解与应用,熟练掌握是关键。

练习册系列答案
相关题目
已知直线
 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
对任意 ,不等式
,不等式 恒成立的一个充分不必要条件是( )
恒成立的一个充分不必要条件是( )
A. | B. | C. | D. |
“ ”是“直线
”是“直线 和线
和线 垂直”的
垂直”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若a,b∈R,则a>b>0是a2>b2的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知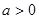 ,则
,则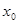 满足关于
满足关于 的方程
的方程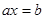 的充要条件是( )
的充要条件是( )
A.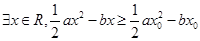 | B. |
C. | D.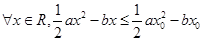 |
命题 :“任意非零向量
:“任意非零向量 ,都有
,都有 ”,则
”,则
A. 是假命题; 是假命题; :任意非零向量 :任意非零向量 ,都有 ,都有 |
B. 是假命题; 是假命题; :存在非零向量 :存在非零向量 ,使 ,使 |
C. 是真命题; 是真命题; :任意非零向量 :任意非零向量 ,都有 ,都有 |
D. 是真命题; 是真命题; :存在非零向量 :存在非零向量 ,使 ,使 |
“1<a<2”是“对任意的正数x,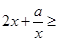 2”的
2”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若一个数是负数,则它的平方是正数”的逆命题是 ( )
| A.“若一个数是负数,则它的平方不是正数” |
| B.“若一个数的平方是正数,则它是负数” |
| C.“若一个数不是负数,则它的平方不是正数” |
| D.“若一个数的平方不是正数,则它不是负数” |