题目内容
4．已知复数z的实部为-1，虚部为2，则$\frac{5i}{z}$的共轭复数是（ ）| A． | 2-i | B． | 2+i | C． | -2-i | D． | -2+i |
分析 由已知得到z，代入$\frac{5i}{z}$，利用复数代数形式的乘除运算化简得答案．
解答 解：由题意可得z=-1+2i，
则$\frac{5i}{z}$=$\frac{5i}{-1+2i}=\frac{5i（-1-2i）}{（-1+2i）（-1-2i）}=\frac{10-5i}{5}=2-i$，
∴$\frac{5i}{z}$的共轭复数是2+i．
故选：B．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
如图，设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，A，B分别为椭圆C的左、右顶点，F为右焦点．直线y=6x与C的交点到y轴的距离为 $\frac{2}{7}$，过点B作x轴的垂线l，D为l 上异于点B的一点，以BD为直径作圆E．
16．已知等差数列{an}的公差d∈（-1，0），且$\frac{si{n}^{2}{a}_{3}co{s}^{2}{a}_{6}-co{s}^{2}{a}_{3}si{n}^{2}{a}_{6}}{sin（{a}_{2}+{a}_{7}）}$=1，仅当n=9时，数列{an}的前n项和Sn取得最大值，则首项a1的取值范围是（ ）
| A． | （$\frac{7π}{6}$，$\frac{4π}{3}$） | B． | [$\frac{7π}{6}$，$\frac{4π}{3}$] | C． | （$\frac{4π}{3}$，$\frac{3π}{2}$） | D． | [$\frac{4π}{3}$，$\frac{3π}{2}$] |
13．如图所示的程序框图，输出的结果S的值为（ ）
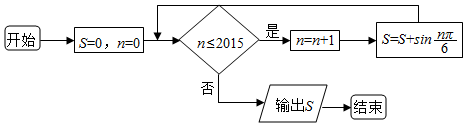
| A． | 0 | B． | $\frac{1}{2}$ | C． | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | D． | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$ |