题目内容
如图,已知直三棱柱![]() 中,
中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.现设
的中点.现设![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的正切值.
的正切值.
解法1:(1)取AB的中点H,连结DH

![]()
![]()
![]() 四边形CHDE为平行四边形.
四边形CHDE为平行四边形.

(2)在等腰![]()
又∵直三棱柱ABC―A1B1C1中,平面ABC⊥平面CBB1C1,
且平面ABC∩平面CBB1C1=CB,
∴AF⊥平面CBB1C1,
又![]() 平面
平面![]() .
.
由题设,CE=a,则![]() ,
,
![]() .
.
 ,
,
![]()
又![]() 平面AEF.
平面AEF.
(3)在平面B1EA内,作![]() ,垂足为K,连结KF.
,垂足为K,连结KF.
则![]() 为二面角B1―AE―F的平面角.
为二面角B1―AE―F的平面角.
∵在Rt△AFE中,![]() ,
,
![]() ,
,
![]()
∴在Rt△B1FK中, .
.
即二面角B1―AE―F的平面角的正切值为![]() .
.
解法2:如图建立空间直角坐标系![]() ,则
,则

![]() ,
,
![]() .
.
(1) 取![]() 的中点H,连结CH.
的中点H,连结CH.
![]() ,
,
![]() ,
,
![]() 平面ABC,
平面ABC,
而![]() 平面
平面![]() ,
,
![]() 平面ABC.
平面ABC.
(2)![]() ,
,
![]()

∴B1F⊥EF,B1F⊥AF.
∵EF∩AF=F.
∴B1F⊥平面AEF.
(3)设平面AB1E的一个法向量为![]()
![]() ,
,
![]() ,
,
 令
令![]() ,则
,则![]() .
.
由于平面AEF的一个法向量为![]() ,
,
故设![]() 与m所成角为θ.
与m所成角为θ.
 .
.
由于平面AB1E与平面AEF所成的二面角为锐二面角.
∴二面角B1―AE―F的平面角的余弦值为![]() .
.
∴二面角B1―AE―F的正切值为![]() .
.

练习册系列答案
相关题目

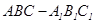 中,
中,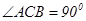 ,
, 是棱
是棱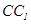 上的动点,
上的动点,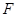 是
是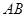 的中点,
的中点,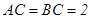 ,
,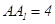 .
.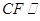 平面
平面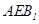 ;
;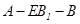 的大小是
的大小是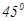 ?若存在,求出
?若存在,求出 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.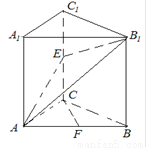
 中,
中, ,
,  ,
,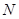 分别是棱
分别是棱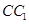 ,
,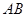 的中点.
的中点. 平面
平面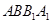 ;
;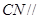 平面
平面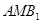 ;
;
 中,
中,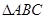 为等腰直角三角形,
为等腰直角三角形,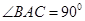 ,且
,且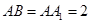 ,
, 分别为
分别为 的中点。
的中点。 //平面
//平面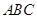 ;
;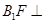 平面
平面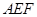 ;
;
