题目内容
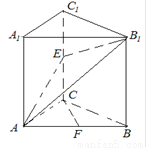
如图,已知直三棱柱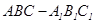 中,
中,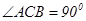 ,
,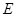 是棱
是棱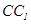 上的动点,
上的动点,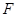 是
是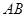 的中点,
的中点,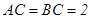 ,
,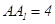 .
.
(1)当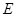 是棱
是棱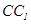 的中点时,求证:
的中点时,求证: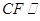 平面
平面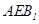 ;
;
(2)在棱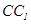 上是否存在点
上是否存在点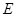 ,使得二面角
,使得二面角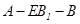 的大小是
的大小是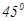 ?若存在,求出
?若存在,求出 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
【答案】
见解析
【解析】本试题主要是考查了空间立体几何中线面的平行和二面角的求解运算,能合理的建立直角坐标系,是解决第二问的关键所在。
(1)证法1 取 中点
中点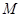 -----------(1分)因
-----------(1分)因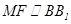 且
且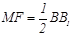 ,
,
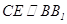 且
且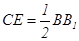 ,故
,故 且
且 , (3分)
, (3分)
因而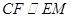 且
且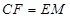 因此
因此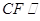 平面
平面 。---------------(2分)
。---------------(2分)
证法2
以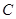 为坐标原点,射线
为坐标原点,射线 为
为 轴正半轴,建立如图所示的空间直角坐标系
轴正半轴,建立如图所示的空间直角坐标系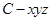 .
.

则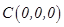 ,
,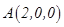 ,
,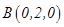 ,
,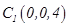 ,
,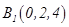 ,
, .
.
设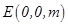 ,平面
,平面 的法向量为
的法向量为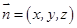 ,
,
依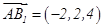 ,
,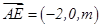
且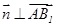 ,
,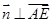 .
.
可得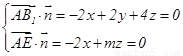
取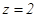 ,得
,得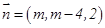 ------------(4分)
------------(4分)
当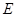 是棱
是棱 的中点时,
的中点时,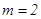 .
.
则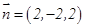 及
及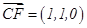 得
得 
故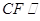 平面
平面 .---------------------------------------------------(2分)
.---------------------------------------------------(2分)
(2)因平面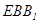 的法向量为
的法向量为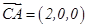 , -------------------------(2分)
, -------------------------(2分)
又二面角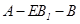 的大小是
的大小是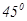 ,故
,故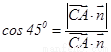
即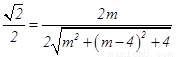 解得
解得 .
.
故在棱 上存在点
上存在点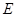 ,使得二面角
,使得二面角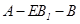 的大小是
的大小是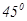 .此时
.此时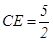 .(4分)
.(4分)

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

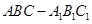 中,
中,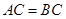 ,
, 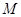 ,
,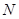 分别是棱
分别是棱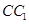 ,
,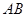 的中点.
的中点. 平面
平面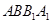 ;
;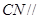 平面
平面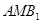 ;
;
 中,
中,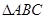 为等腰直角三角形,
为等腰直角三角形,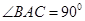 ,且
,且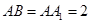 ,
, 分别为
分别为 的中点。
的中点。 //平面
//平面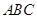 ;
;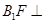 平面
平面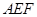 ;
;
