题目内容
5.已知函数$f(x)=\frac{1}{a}-\frac{1}{x};(a>0)$.(1)证明f(x)在(0,+∞)上单调递增;
(2)是否存在实数a使得f(x)的定义域、值域都是$[{\frac{1}{2},2}]$,若存在求出a的值,若不存在说明理由.
分析 (1)根据函数的单调性的定义证明即可;
(2)根据函数的单调性得到关于a的方程组,解出即可.
解答 (1)证明:设x2>x1>0,
则f(x2)-f(x1)=($\frac{1}{a}$-$\frac{1}{{x}_{2}}$)-($\frac{1}{a}$-$\frac{1}{{x}_{1}}$)=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{{{x}_{2}-x}_{1}}{{{x}_{1}x}_{2}}$,
∵x2>x1>0,∴x2-x1>0,
∴$\frac{{{x}_{2}-x}_{1}}{{{x}_{1}x}_{2}}$>0,即f(x2)>f(x1),
∴f(x)在(0,+∞)递增;
(2)解:∵f(x)在(0,+∞)递增,
且定义域和值域均是[$\frac{1}{2}$,2],
∴$\left\{{\begin{array}{l}{f(\frac{1}{2})=\frac{1}{a}-2=\frac{1}{2}}\\{f(2)=\frac{1}{a}-\frac{1}{2}=2}\end{array}}\right.$,
所以存在实数$a=\frac{2}{5}$.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
20.函数f(x)=$\left\{\begin{array}{l}lg|x-2|(x≠2)\\ 1(x=2)\end{array}\right.$若关于x的方程[f(x)]2+b•f(x)+c=0恰有5个不同的实数解x1、x2、x3、x4、x5,则f(x1+x2+x3+x4+x5)等于( )
| A. | 0 | B. | 1 | C. | lg4 | D. | 3lg2 |
15.如果$\overrightarrow{e_1}$,$\overrightarrow{e_2}$是平面内所有向量的一组基底,那么( )
| A. | 该平面内存在一向量$\overrightarrow a$不能表示$\overrightarrow a=m\overrightarrow{e_1}+n\overrightarrow{e_2}$,其中m,n为实数 | |
| B. | 若向量$m\overrightarrow{e_1}+n\overrightarrow{e_2}$与$\overrightarrow a$共线,则存在唯一实数λ使得$m\overrightarrow{e_1}+n\overrightarrow{e_2}=λ\overrightarrow a$ | |
| C. | 若实数m,n使得$m\overrightarrow{e_1}+n\overrightarrow{e_2}=\overrightarrow 0$,则m=n=0 | |
| D. | 对平面中的某一向量$\overrightarrow a$,存在两对以上的实数m,n使得$\overrightarrow a=m\overrightarrow{e_1}+n\overrightarrow{e_2}$ |
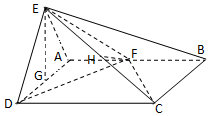 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.