题目内容
已知复数z=（a2-7a+12）+（a2-5a+6）i（a∈R），那么当a为何值时，z是实数？当a为何值时，z是虚数？当a为何值时，z是纯虚数？
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：①由复数z的虚部等于0求解a的值；
②由复数z的虚部不等于0求解a的值；
③复数z的实部等于0且虚部不等于0联立求解m的值．
②由复数z的虚部不等于0求解a的值；
③复数z的实部等于0且虚部不等于0联立求解m的值．
解答：
解：①当a2-5a+6=0，即m=2或a=3时，z是实数；
②当a2-5a+6≠0，即a≠2且a≠3时，z是虚数；
③当a2-7a+12=0，且a2-5a+6≠0，即a=4时，z是纯虚数．
②当a2-5a+6≠0，即a≠2且a≠3时，z是虚数；
③当a2-7a+12=0，且a2-5a+6≠0，即a=4时，z是纯虚数．
点评：本题考查了复数的基本概念，考查了复数是实数、虚数和纯虚数的条件，是基础题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
cos（-
）的值是（ ）
| π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若数据x1，x2，…，xn的方差是1，则若数据2x1-3，2x2-3，…，2xn-3的方差是（ ）
| A、-1 | B、1 | C、2 | D、4 |
某企业生产一种汽车配件，经抽样统计，该企业生产的配件尺寸的样本频率分布直方图如下．配件尺寸在[60，62）内的为一等品，尺寸在[58，60）或[62，64）内的为二等品，其余为三等品．用频率近似表示概率．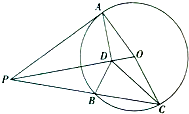
如图，AP是圆O的切线，A是切点，AD⊥OP与D点，过点P作圆O的割线与圆O相交于B，C两点