题目内容
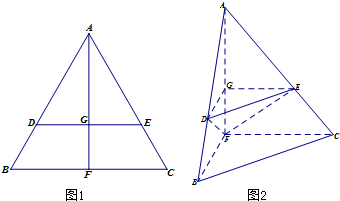 (2013•广东)如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=
(2013•广东)如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=
| ||
| 2 |
(1)证明:DE∥平面BCF;
(2)证明:CF⊥平面ABF;
(3)当AD=
| 2 |
| 3 |
分析:(1)在等边三角形ABC中,由AD=AE,可得
=
,在折叠后的三棱锥A-BCF中也成立,故有DE∥BC,再根据直线和平面平行的判定定理证得DE∥平面BCF.
(2)由条件证得AF⊥CF ①,且BF=CF=
.在三棱锥A-BCF中,由BC=
,可得BC2=BF2+CF2,从而 CF⊥BF②,结合①②,证得CF⊥平面ABF.
(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.再由 VF-DEG=VE-DFG=
•
•DG•FG•GE,运算求得结果.
| AD |
| DB |
| AE |
| EC |
(2)由条件证得AF⊥CF ①,且BF=CF=
| 1 |
| 2 |
| ||
| 2 |
(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.再由 VF-DEG=VE-DFG=
| 1 |
| 3 |
| 1 |
| 2 |
解答:解:(1)在等边三角形ABC中,AD=AE,∴
=
,在折叠后的三棱锥A-BCF中也成立,
∴DE∥BC.
又∵DE?平面BCF,BC?平面BCF,
∴DE∥平面BCF.
(2)在等边三角形ABC中,F是BC的中点,所以AF⊥BC,即AF⊥CF ①,且BF=CF=
.
∵在三棱锥A-BCF中,BC=
,∴BC2=BF2+CF2,∴CF⊥BF②.
又∵BF∩AF=F,∴CF⊥平面ABF.
(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.
∴VF-DEG=VE-DFG=
•
•DG•FG•GE=
•
•
•(
•
)•
=
.
| AD |
| DB |
| AE |
| EC |
∴DE∥BC.
又∵DE?平面BCF,BC?平面BCF,
∴DE∥平面BCF.
(2)在等边三角形ABC中,F是BC的中点,所以AF⊥BC,即AF⊥CF ①,且BF=CF=
| 1 |
| 2 |
∵在三棱锥A-BCF中,BC=
| ||
| 2 |
又∵BF∩AF=F,∴CF⊥平面ABF.
(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.
∴VF-DEG=VE-DFG=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 324 |
点评:本题主要考查直线和平面平行的判定定理、直线和平面垂直的判定的定理的应用,用等体积法求三棱锥的体积,属于中档题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
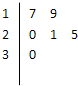 (2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
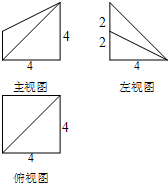 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为