题目内容
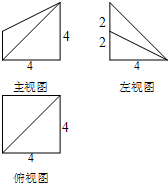 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为| 80 |
| 3 |
| 80 |
| 3 |
分析:由三视图还原得到原几何体,然后等过分割几何体为两个三棱锥,由棱锥的体积得到原几何体的体积.
解答: 解:由三视图可得原几何体如图,
解:由三视图可得原几何体如图,
其中底面ABCD为边长为4的正方形,AF,DE均与底面垂直,
且AF=2,DE=4.
求该几何体的体积,可连结BD,
则VABCDEF=VE-BCD+VB-ADEF
=
SBCD•DE+
SADEF•AB
=
×
×4×4×4+
×
(2+4)×4×4
=
.
故答案为
.
 解:由三视图可得原几何体如图,
解:由三视图可得原几何体如图,其中底面ABCD为边长为4的正方形,AF,DE均与底面垂直,
且AF=2,DE=4.
求该几何体的体积,可连结BD,
则VABCDEF=VE-BCD+VB-ADEF
=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 80 |
| 3 |
故答案为
| 80 |
| 3 |
点评:本题考查了由三视图求原几何体的体积,考查了由三视图还原原几何体,由三视图还原原几何体,首先看俯视图,然后结合主视图和左视图得原图形,训练了利用分割图形法求几何体的体积,是基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目