题目内容
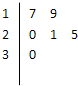 (2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
分析:(1)茎叶图中共同的数字是数字的十位,这是解决本题的突破口,根据所给的茎叶图数据,代入平均数公式求出结果;
(2)先由(1)求得的平均数,再利用比例关系即可推断该车间12名工人中有几名优秀工人的人数;
(3)设“从该车间12名工人中,任取2人,恰有1名优秀工人”为事件A,结合组合数利用概率的计算公式即可求解事件A的概率.
(2)先由(1)求得的平均数,再利用比例关系即可推断该车间12名工人中有几名优秀工人的人数;
(3)设“从该车间12名工人中,任取2人,恰有1名优秀工人”为事件A,结合组合数利用概率的计算公式即可求解事件A的概率.
解答:解:(1)样本均值为
=22
(2)抽取的6名工人中有2名为优秀工人,
所以12名工人中有4名优秀工人
(3)设“从该车间12名工人中,任取2人,恰有1名优秀工人”为事件A,
所以P(A)=
=
,
即恰有1名优秀工人的概率为
.
| 17+19+20+21+25+30 |
| 6 |
(2)抽取的6名工人中有2名为优秀工人,
所以12名工人中有4名优秀工人
(3)设“从该车间12名工人中,任取2人,恰有1名优秀工人”为事件A,
所以P(A)=
| ||||
|
| 16 |
| 33 |
即恰有1名优秀工人的概率为
| 16 |
| 33 |
点评:本题主要考查茎叶图的应用,古典概型及其概率计算公式,属于容易题.对于一组数据,通常要求的是这组数据的众数,中位数,平均数,题目分别表示一组数据的特征,考查最基本的知识点.

练习册系列答案
相关题目
 (2013•广东)某四棱台的三视图如图所示,则该四棱台的体积是( )
(2013•广东)某四棱台的三视图如图所示,则该四棱台的体积是( )
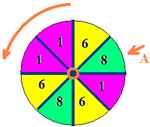 (2013•广东模拟)如图,转盘游戏.转盘被分成8个均匀的扇形区域.游戏规则:用力旋转转盘,转盘停止时箭头A所指区域的数字就是游戏所得的点数(转盘停留的位置是随机的).假设箭头指到区域分界线的概率为
(2013•广东模拟)如图,转盘游戏.转盘被分成8个均匀的扇形区域.游戏规则:用力旋转转盘,转盘停止时箭头A所指区域的数字就是游戏所得的点数(转盘停留的位置是随机的).假设箭头指到区域分界线的概率为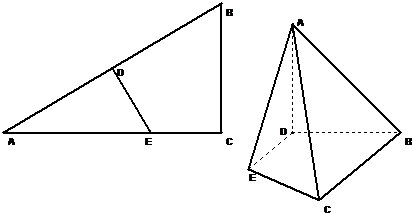 (2013•广东模拟)在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,D、E分别为AB、AC上的点,AB⊥DE,沿DE将△ADE折起,使得平面ADE⊥平面BDEC,设AD=x.
(2013•广东模拟)在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,D、E分别为AB、AC上的点,AB⊥DE,沿DE将△ADE折起,使得平面ADE⊥平面BDEC,设AD=x.