题目内容
15．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+ax-2，x≤1}\\{-{a}^{x}，x＞1}\end{array}\right.$，且a≠1在（0，+∞）上是增函数，则a的取值范围是（ ）| A． | （0，$\frac{1}{2}$） | B． | （0，1） | C． | $（0，\frac{1}{2}]$ | D． | $[\frac{1}{2}，1）$ |
分析 利用函数在（0，+∞）上是增函数，列出不等式组，求解即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+ax-2，x≤1}\\{-{a}^{x}，x＞1}\end{array}\right.$，且a≠1）在（0，+∞）上是增函数，
可得：$\left\{\begin{array}{l}{0＜a＜1}\\{-\frac{a}{2}＜0}\\{-a≥a-1}\end{array}\right.$，解得a∈$（0，\frac{1}{2}]$．
故选：C．
点评 本题考查分段函数的应用，函数的单调性的应用，考查转化思想以及计算能力．
练习册系列答案
相关题目
5．函数f（x）的定义域为R，导函数f'（x）的图象如图所示，则函数f（x）（ ）
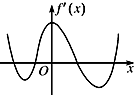
| A． | 无极大值点，有四个极小值点 | B． | 有三个极大值点，两个极小值点 | ||
| C． | 有两个极大值点，两个极小值点 | D． | 有四个极大值点，无极小值点 |
6．已知a，b∈R，那么a+b≠0的一个必要而不充分条件是（ ）
| A． | ab＞0 | B． | a＞0且b＞0 | C． | a+b＞3 | D． | a≠0或b≠0 |
10．若实数a，b，c满足loga3＜logb3＜logc3，则下列关系中不可能成立的（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | c＜b＜a | D． | a＜c＜b |
20．已知命题p：?x∈[0，2π]，sinx≤1，则（ ）
| A． | ￢p：?x∈[0，2π]，sinx≥1 | B． | ￢p：?x∈[-2π，0]，sinx＞1 | ||
| C． | ￢p：?x∈[0，2π]，sinx＞1 | D． | ￢p：?x∈[-2π，0]，sinx＞1 |
7．在等腰直角△ABC中，AC=BC，D在AB边上且满足：$\overrightarrow{CD}=t\overrightarrow{CA}+（1-t）\overrightarrow{CB}$，若∠ACD=60°，则t的值为（ ）
| A． | $\frac{{\sqrt{3}-1}}{2}$ | B． | $\sqrt{3}-1$ | C． | $\frac{{\sqrt{3}-\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}+1}}{2}$ |
5．
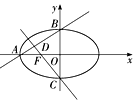如图所示，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左焦点为F，A、B、C为其三个顶点，直线CF与AB交于D点，则tan∠ADF的值等于（ ）
如图所示，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左焦点为F，A、B、C为其三个顶点，直线CF与AB交于D点，则tan∠ADF的值等于（ ）| A． | 3$\sqrt{3}$ | B． | -3$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{5}$ | D． | -$\frac{\sqrt{3}}{5}$ |