题目内容
设a，b，c，d∈R，且a＞b，c＞d，则下列结论中正确的是（ ）
| A、a+c＞b+d |
| B、a-c＞b-d |
| C、ac＞bd |
| D、ad＞bc |
考点：不等关系与不等式
专题：不等式的解法及应用
分析：根据不等式的基本性质，对四个选项进行分析、判断，即可得出正确的答案．
解答：
解：∵a，b，c，d∈R，且a＞b，c＞d，
根据同向不等式的可加性，得；
a+c＞b+d，∴A正确．
故选：A．
根据同向不等式的可加性，得；
a+c＞b+d，∴A正确．
故选：A．
点评：本题考查了不等式的基本性质的应用问题，解题时宜用直接法选出正确的答案，是基础题目．
练习册系列答案
相关题目
如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是（ ）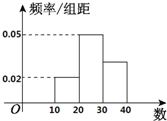 
| A、25；25 |
| B、26；25 |
| C、26；26 |
| D、25；26 |
动点P（x，0），定点A（0，2），B（4，1），则|PA|+|PB|的最小值为（ ）
A、
| ||
B、3
| ||
| C、4 | ||
| D、5 |
函数y=f（x）在R上为增函数，且f（2m）＞f（-m+6），则实数m的取值范围是（ ）
| A、（-∞，-2） |
| B、（0，+∞） |
| C、（2，+∞） |
| D、（-∞，-2）∪（2，+∞） |