题目内容
设双曲线 的半焦距为c,已知直线l过(a,0),(0,b)两点,且原点O到直线l的距离为
的半焦距为c,已知直线l过(a,0),(0,b)两点,且原点O到直线l的距离为 ,求此双曲线的离心率.
,求此双曲线的离心率.
【答案】分析:先求出直线l的方程,利用原点到直线l的距离为  ,及又c2=a2+b2,求出离心率的平方e2,进而求出离心率.
,及又c2=a2+b2,求出离心率的平方e2,进而求出离心率.
解答:解:由题设条件知直线l的方程为 即:ay+bx-ab=0
即:ay+bx-ab=0
∵原点O到直线l的距离为 ∴
∴ (4分)
(4分)
又c2=a2+b2∴ 从而16a2(c2-a2)=3c4(6分)
从而16a2(c2-a2)=3c4(6分)
∵a>0∴3e4-16e2+16=0解得:e2=4或 (8分)
(8分)
∵0<a<b∴ (10分)
(10分)
∴e2=4又e>1
所以此双曲线的离心率为2(12分)
点评:本题考查双曲线性质.主要考查求双曲线的离心率常用的方法,注意椭圆中三参数的关系是:a2=b2+c2双曲线中三参数的关系:c2=b2+a2.的不同之处.
 ,及又c2=a2+b2,求出离心率的平方e2,进而求出离心率.
,及又c2=a2+b2,求出离心率的平方e2,进而求出离心率.解答:解:由题设条件知直线l的方程为
 即:ay+bx-ab=0
即:ay+bx-ab=0∵原点O到直线l的距离为
 ∴
∴ (4分)
(4分)又c2=a2+b2∴
 从而16a2(c2-a2)=3c4(6分)
从而16a2(c2-a2)=3c4(6分)∵a>0∴3e4-16e2+16=0解得:e2=4或
 (8分)
(8分)∵0<a<b∴
 (10分)
(10分)∴e2=4又e>1
所以此双曲线的离心率为2(12分)
点评:本题考查双曲线性质.主要考查求双曲线的离心率常用的方法,注意椭圆中三参数的关系是:a2=b2+c2双曲线中三参数的关系:c2=b2+a2.的不同之处.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设双曲线的半焦距为c,两条准线间的距离为d,且c=d,那么双曲线的离心率e等于( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
 的半焦距为c,直线l过
的半焦距为c,直线l过 两点,若原点O到l的距离为
两点,若原点O到l的距离为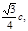 则双曲线的离心率为( )
则双曲线的离心率为( )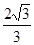 或2 B.2 C.
或2 B.2 C. 或
或 的半焦距为c.已知原点到直线l:bx+ay=ab的距离等于
的半焦距为c.已知原点到直线l:bx+ay=ab的距离等于 ,则c的最小值为 .
,则c的最小值为 .