题目内容
设双曲线
的半焦距为c．已知原点到直线l：bx+ay=ab的距离等于
，则c的最小值为 ．
【答案】分析：先根据点到直线的距离求得知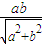
=
=
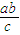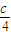+1，进而根据均值不等式的性质求得ab≤
=
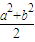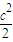求得c的范围．
解答：解：依题意可知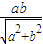
=
=
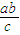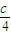+1
∴ab=
c2+c
∵ab≤
=
∴
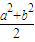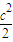
c2+c≤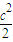
，解得c≥4或c≤0（舍去）
故答案为4
点评：本题主要考查了直线与圆锥曲线的综合问题．解题的关键是利用点到直线的距离求得a，b和c的关系．
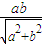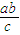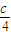==+1，进而根据均值不等式的性质求得ab≤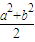=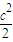求得c的范围．解答：解：依题意可知
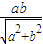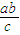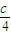==+1∴ab=
c2+c∵ab≤
=∴
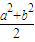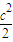
c2+c≤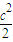，解得c≥4或c≤0（舍去）故答案为4
点评：本题主要考查了直线与圆锥曲线的综合问题．解题的关键是利用点到直线的距离求得a，b和c的关系．
练习册系列答案
阅读快车系列答案
相关题目
设双曲线的半焦距为c，两条准线间的距离为d，且c=d，那么双曲线的离心率e等于（ ）
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
的半焦距为C，直线L过
两点，已知原点到直线L的距离为
，则双曲线的离心率为
C 
D 
的半焦距为c，直线l过
两点，若原点O到l的距离为
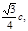则双曲线的离心率为( )
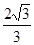或2 B.2 C.
或