题目内容
已知函数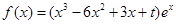 ,
, .
.
(Ⅰ)若函数 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的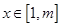 ,不等式
,不等式 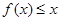 恒成立.求正整数
恒成立.求正整数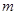 的最大值.
的最大值.
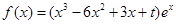 ,
, .
.(Ⅰ)若函数
 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;(Ⅱ)若存在实数
 ,使对任意的
,使对任意的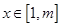 ,不等式
,不等式 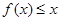 恒成立.求正整数
恒成立.求正整数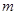 的最大值.
的最大值.(1) (2)整数m的最大值为5
(2)整数m的最大值为5
 (2)整数m的最大值为5
(2)整数m的最大值为5第一问中利用导数在在 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的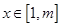 ,不等式
,不等式  恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式 ,即
,即 ,即
,即 .
.
转化为存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在 上恒成立.
上恒成立.
即不等式 在
在 上恒成立.
上恒成立.
设 ,则.
,则.
设 ,则
,则 ,因为
,因为 ,有
,有 .
.
故 在区间
在区间 上是减函数。又
上是减函数。又
故存在 ,使得
,使得 .
.
当 时,有
时,有 ,当
,当 时,有
时,有 .
.
从而 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.
又

所以当 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;
故使命题成立的正整数m的最大值为5
 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。第二问中,利用存在实数
 ,使对任意的
,使对任意的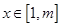 ,不等式
,不等式  恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。解:(1)
①

(2)不等式
 ,即
,即 ,即
,即 .
.转化为存在实数
 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立.
恒成立.即不等式
 在
在 上恒成立.
上恒成立.即不等式
 在
在 上恒成立.
上恒成立.设
 ,则.
,则.
设
 ,则
,则 ,因为
,因为 ,有
,有 .
.故
 在区间
在区间 上是减函数。又
上是减函数。又
故存在
 ,使得
,使得 .
.当
 时,有
时,有 ,当
,当 时,有
时,有 .
.从而
 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.又


所以当
 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;故使命题成立的正整数m的最大值为5

练习册系列答案
相关题目
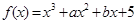 ,过曲线
,过曲线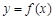 上的点
上的点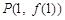 的切线斜率为3.
的切线斜率为3.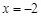 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;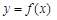 在
在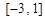 上最大值;
上最大值;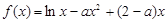 .
.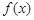 的单调性;
的单调性;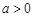 ,证明:当
,证明:当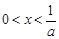 时,
时,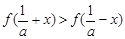 ;
;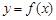 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,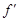 (x0)<0.
(x0)<0.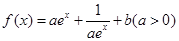
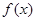 在
在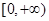 上的最小值;
上的最小值;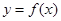 在点
在点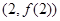 的切线方程为
的切线方程为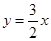 ;求
;求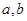 的值。
的值。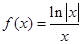
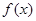 的单调区间; (II)若关于
的单调区间; (II)若关于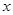 的不等式
的不等式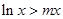 对一切
对一切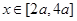 都成立
都成立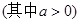 ,求实数
,求实数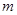 的取值范围.
的取值范围.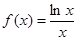 ,若方程
,若方程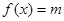 存在两个不同的实数解,则实数
存在两个不同的实数解,则实数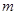 的取值范围为( ▲ )
的取值范围为( ▲ )



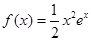 .
.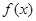 的单调区间;
的单调区间; 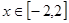 时,不等式
时,不等式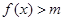 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.