题目内容
已知向量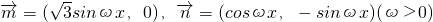 ,在函数
,在函数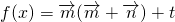 的图象上,对称中心到对称轴的最小距离为
的图象上,对称中心到对称轴的最小距离为 ,且当
,且当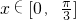 时f(x)的最小值为
时f(x)的最小值为 .
.
(1)求f(x)的解析式;
(2)求f(x)的单调递增区间;
(3)若对任意x1,x2∈[0, ]都有|f(x1)-f(x2)|<m,求实数m的取值范围.
]都有|f(x1)-f(x2)|<m,求实数m的取值范围.
解:(1)∵ ,
,
∴
= =
= =
= ,
,
由题意可得 ,∴ω=1.
,∴ω=1.
∵ ,∴
,∴ .
.
又f(x)的最小值为 =
= ×(
×( )+
)+ +t,
+t,
∴ ,
,
故 .
.
(2)令 ,可得
,可得 ,
,
∴ ,
,
即单调递增区间为: .
.
(3)当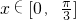 时,f(x)的最大值为
时,f(x)的最大值为  ×(
×( )+
)+ +
+ =
= ,最小值为
,最小值为 ,
,
∴|f(x1)-f(x2)|的最大值为 =3.
=3.
∵对任意x1,x2∈[0, ]都有|f(x1)-f(x2)|<m,
]都有|f(x1)-f(x2)|<m,
∴m>3,即实数m的取值范围为(3,+∞).
分析:(1)化简函数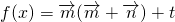 的解析式,根据它的
的解析式,根据它的 周期等于
周期等于 ,求出ω的值,再根据当
,求出ω的值,再根据当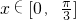 时f(x)的最小值为
时f(x)的最小值为 ,求出t的值,即可得到f(x)的解析式.
,求出t的值,即可得到f(x)的解析式.
(2)令 ,解出x的范围,即可得到单调递增区间.
,解出x的范围,即可得到单调递增区间.
(3)当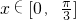 时,求得f(x)的最大值为
时,求得f(x)的最大值为  ,最小值为
,最小值为 ,可得|f(x1)-f(x2)|的最大值为3,由此得到实数m的取值范围.
,可得|f(x1)-f(x2)|的最大值为3,由此得到实数m的取值范围.
点评:本题主要考查三角函数的恒等变换及化简求值,两个向量的数量积的定义,正弦函数的定义域和值域、周期性及单调性的应用,属于中档题.
 ,
,∴

=
 =
= =
= ,
,由题意可得
 ,∴ω=1.
,∴ω=1. ∵
 ,∴
,∴ .
.又f(x)的最小值为
 =
= ×(
×( )+
)+ +t,
+t,∴
 ,
,故
 .
.(2)令
 ,可得
,可得 ,
,∴
 ,
,即单调递增区间为:
 .
.(3)当
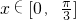 时,f(x)的最大值为
时,f(x)的最大值为  ×(
×( )+
)+ +
+ =
= ,最小值为
,最小值为 ,
,∴|f(x1)-f(x2)|的最大值为
 =3.
=3.∵对任意x1,x2∈[0,
 ]都有|f(x1)-f(x2)|<m,
]都有|f(x1)-f(x2)|<m,∴m>3,即实数m的取值范围为(3,+∞).
分析:(1)化简函数
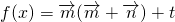 的解析式,根据它的
的解析式,根据它的 周期等于
周期等于 ,求出ω的值,再根据当
,求出ω的值,再根据当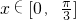 时f(x)的最小值为
时f(x)的最小值为 ,求出t的值,即可得到f(x)的解析式.
,求出t的值,即可得到f(x)的解析式.(2)令
 ,解出x的范围,即可得到单调递增区间.
,解出x的范围,即可得到单调递增区间.(3)当
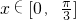 时,求得f(x)的最大值为
时,求得f(x)的最大值为  ,最小值为
,最小值为 ,可得|f(x1)-f(x2)|的最大值为3,由此得到实数m的取值范围.
,可得|f(x1)-f(x2)|的最大值为3,由此得到实数m的取值范围.点评:本题主要考查三角函数的恒等变换及化简求值,两个向量的数量积的定义,正弦函数的定义域和值域、周期性及单调性的应用,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目

 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像. ,
,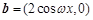
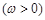 ,函数
,函数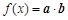 的图象与直线
的图象与直线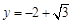 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为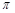 .
.
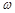 的值;
的值; 在
在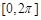 上的单调递增区间.
上的单调递增区间.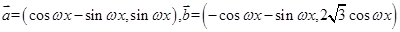 ,设函数
,设函数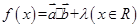 的图象关于直线
的图象关于直线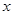 =π对称,其中
=π对称,其中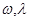 为常数,且
为常数,且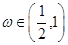 .
.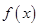 的最小正周期;
的最小正周期;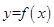 的图象经过点
的图象经过点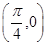 ,求函数
,求函数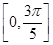 上的取值范围.
上的取值范围. ,在函数
,在函数 的图象上,对称中心到对称轴的最小距离为
的图象上,对称中心到对称轴的最小距离为 ,且当
,且当 时f(x)的最小值为
时f(x)的最小值为 .
. ]都有|f(x1)-f(x2)|<m,求实数m的取值范围.
]都有|f(x1)-f(x2)|<m,求实数m的取值范围.