题目内容
已知向量
，设函数
的图象关于直线
对称，其中常数
(Ⅰ)求
的最小正周期；
(Ⅱ)将函数的图像向左平移
个单位，得到函数
的图像，用五点法作出函数在区间
的图像.
【答案】
(Ⅰ)
；(Ⅱ)详见解析.
【解析】
试题分析：(Ⅰ)由向量的数量积的坐标表示将
表示出来，并利用正弦和余弦的二倍角公式将其表示为
的形式，再由对称轴为
，所以在处函数值取到最大值或最小值，从而得
，代入并结合
求
的值，再利用
和的关系，求；(Ⅱ)用
代换
得
，先由
，确定
，从中取特殊点
，
，
，
，
，再计算相应的自变量和函数值
，列表，描点连线，即得在给定区间的图象.
试题解析：(Ⅰ)
，
；
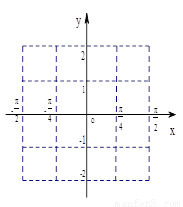
(Ⅱ)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-2 |
0 |
2 |
0 |
考点：1、向量数量积的坐标表示；2、正弦和余弦的二倍角公式；3、五点作图法.
练习册系列答案
相关题目
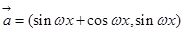
，设函数
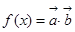
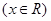的图象关于直线
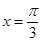对称，其中常数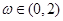
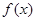的最小正周期；
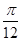个单位，得到函数
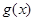的图像，用五点法作出函数
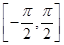的图像.
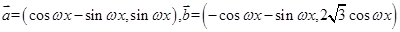，设函数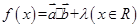
的图象关于直线
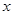=π对称，其中
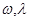为常数，且
．
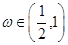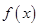的最小正周期；
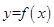的图象经过点
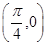，求函数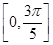
上的取值范围．
,
，设函数
. 
的零点组成公差为
的等差数列，求函数
，（
），求函数
，设函数
的图象关于点
中心对称，其中
为常数，且
.
的最小正周期；
在
上无解，求实数
的取值范围.