题目内容
设点A(2,2),F(4,0),点M在椭圆 上运动.求|MA|+
上运动.求|MA|+ |MF|的最小值.
|MF|的最小值.
解:由题设条件可知,A(2,2)在椭圆 内,
内,
F(4,0)是椭圆 的右焦点,
的右焦点,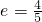 .
.
作PB⊥右准线,且与右准线交于点B,
由椭圆的第二定义可知, ,∴
,∴ .
.
由题意可知,|MA|+ |MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线
|MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线 的距离,
的距离,
其最小值为 .
.
分析:作PB⊥右准线,且与右准线交于点B,由椭圆的第二定义可知, ,∴
,∴ .
.
由题意可知,|MA|+ |MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线
|MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线 的距离.由此可求出|MA|+
的距离.由此可求出|MA|+ |MF|的最小值.
|MF|的最小值.
点评:本题考查椭圆中最小值的求法,借助椭圆的第二定义可以准确求解.
 内,
内,F(4,0)是椭圆
 的右焦点,
的右焦点,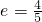 .
.作PB⊥右准线,且与右准线交于点B,
由椭圆的第二定义可知,
 ,∴
,∴ .
.由题意可知,|MA|+
 |MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线
|MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线 的距离,
的距离,其最小值为
 .
.分析:作PB⊥右准线,且与右准线交于点B,由椭圆的第二定义可知,
 ,∴
,∴ .
.由题意可知,|MA|+
 |MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线
|MF|的最小值即|MA|+|MB|的最小值为点A(2,2)到准线 的距离.由此可求出|MA|+
的距离.由此可求出|MA|+ |MF|的最小值.
|MF|的最小值.点评:本题考查椭圆中最小值的求法,借助椭圆的第二定义可以准确求解.

练习册系列答案
相关题目
 已知定点A(-2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的
已知定点A(-2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的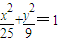 上运动.求|MA|+
上运动.求|MA|+ |MF|的最小值.
|MF|的最小值.