题目内容
 已知定点A(-2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的
已知定点A(-2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的| 1 | 2 |
(1)求点M的轨迹E的方程;
(2)试判断以线段PQ为直径的圆是否经过定点F,并说明理由.
分析:(1)由椭圆的第二定义即可知道点M的轨迹E为椭圆;
(2)设出椭圆上的点C的坐标,进而写出直线AC、BC的方程,分别求出点P、Q的坐标,只要判断kPF•kQF=-1是否成立即可.
(2)设出椭圆上的点C的坐标,进而写出直线AC、BC的方程,分别求出点P、Q的坐标,只要判断kPF•kQF=-1是否成立即可.
解答:解:(1)由椭圆的第二定义可知: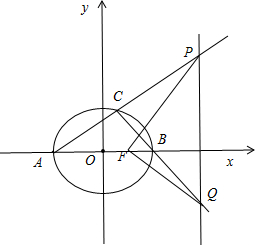
点M的轨迹E是以定点F(1,0)为焦点,离心率e=
,直线l:x=4为准线的椭圆(除去与x轴相交的两点).
∴c=1,
=
,∴a=2,b2=22-12=3,
∴点M的轨迹为椭圆E,其方程为
+
=1(除去(±2,0)).
(2)以线段PQ为直径的圆经过定点F.下面给出证明:
如图所示:设C(x0,y0),(x0≠±2),则直线AC的方程为:y=
(x+2),
令x=4,则yP=
,∴P(4,
),∴kPF=
=
;
直线BC的方程为:y=
(x-2),令x=4,则yQ=
,∴Q(4,
),∴kQF=
=
.
∴kPF•kQF=
×
=
,
∵点C(x0,y0)在椭圆
+
=1上,∴
+
=1,∴
=-1,
∴kPF•kQF=-1.
因此以线段PQ为直径的圆经过定点F.

点M的轨迹E是以定点F(1,0)为焦点,离心率e=
| 1 |
| 2 |
∴c=1,
| c |
| a |
| 1 |
| 2 |
∴点M的轨迹为椭圆E,其方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)以线段PQ为直径的圆经过定点F.下面给出证明:
如图所示:设C(x0,y0),(x0≠±2),则直线AC的方程为:y=
| y0 |
| x0+2 |
令x=4,则yP=
| 6y0 |
| x0+2 |
| 6y0 |
| x0+2 |
| ||
| 4-1 |
| 2y0 |
| x0+2 |
直线BC的方程为:y=
| y0 |
| x0-2 |
| 2y0 |
| x0-2 |
| 2y0 |
| x0-2 |
| ||
| 4-1 |
| 2y0 |
| 3(x0-2) |
∴kPF•kQF=
| 2y0 |
| x0+2 |
| 2y0 |
| 3(x0-2) |
| 4y02 |
| 3(x02-4) |
∵点C(x0,y0)在椭圆
| x2 |
| 4 |
| y2 |
| 3 |
| x02 |
| 4 |
| y02 |
| 3 |
| 4y02 |
| 3(x02-4) |
∴kPF•kQF=-1.
因此以线段PQ为直径的圆经过定点F.
点评:熟练掌握椭圆的定义、直线垂直与斜率的关系是解题的关键.

练习册系列答案
相关题目
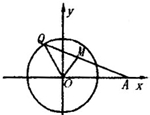 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.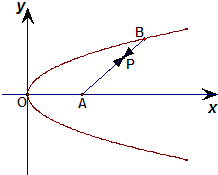 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得