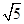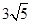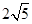题目内容
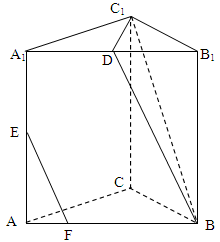
如图,已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点。

(1)求证:直线AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值

(1)求证:直线AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值
(1)见解析;(2) 。
。
 。
。 试题分析:(1) 连B
 C交
C交 于E,连DE, 要证直线AB1∥平面C1DB,证明AB1∥DE即可;(2)根据异面直线所成角的定义并结合(1)可知∠DEB为异面直线
于E,连DE, 要证直线AB1∥平面C1DB,证明AB1∥DE即可;(2)根据异面直线所成角的定义并结合(1)可知∠DEB为异面直线 所成的角,然后用余弦定理求解。
所成的角,然后用余弦定理求解。试题解析:(1)连B
 C交
C交 于E,连DE, 则DE∥
于E,连DE, 则DE∥ ,
,而DE
 面C
面C DB,
DB,
 面C
面C DB, ∴
DB, ∴ 平面C1DB。
平面C1DB。(2)由(1)知∠DEB为异面直线
 所成的角,
所成的角,在

由余弦定理得
 。
。 
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
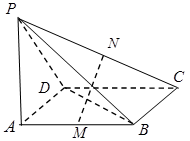

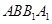 和
和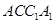 都为矩形。
都为矩形。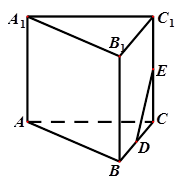
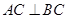 ,证明:直线
,证明:直线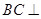 平面
平面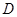 ,
,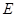 分别是线段
分别是线段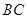 ,
,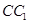 的中点,在线段
的中点,在线段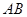 上是否存在一点
上是否存在一点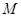 ,使直线
,使直线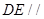 平面
平面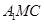 ?请证明你的结论。
?请证明你的结论。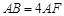 .
.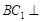 平面
平面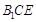 .
.
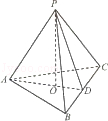
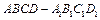 中,
中,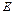 为
为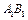 的中点,则异面直线
的中点,则异面直线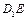 和
和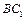 间的距离 .
间的距离 .