Question

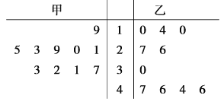
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过300）：

空气质量指数
空气质量等级	1级优	2级良	3级轻度污染	4级中度污染	5级重度污染	6级严重污染

该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率.

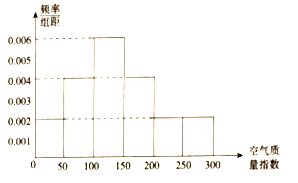
（1）以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况，则2018年11月中有多少天的空气质量达到优良？

（2）从这10天的空气质量指数监测数据中，随机抽取三天，求恰好有一天空气质量良的概率；

（3）从这10天的数据中任取三天数据，记表示抽取空气质量良的天数，求的分布列和期望.

Answer 1

【答案】（1）11月中平均有9天的空气质量达到优良；（2）；（3）见解析

【解析】

（1）由频率分布直方图得到11月中10天的空气质量优良的频率，即为概率，然后进行估计可得30天中空气优良的天数．（2）根据古典概型概率公式和组合数的计算可得所求概率．（3）先判断出随机变量的所有可能取值，然后分别求出对应的概率，进一步可得分布列和期望．

（1）由频率分布直方图，知这10天中1级优1天，2级良2天，3-6级共7天.

所以这10天中空气质量达到优良的概率为，

因为，

所以11月中平均有9天的空气质量达到优良．

（2）记“从10天的空气质量指数监测数据中，随机抽取三天，恰有一天空气质量优良”为事件，

则，

即恰好有一天空气质量良的概率．

（3）由题意得的所有可能取值为0，1，2，

；

；

．

所以的分布列为：

	0	1	2

所以．