题目内容
 截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:
截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:| 驾校A | 驾校B | 驾校C | |
| 人数 | 150 | 200 | 250 |
| 87 | 97 | 91 | 92 | 93 | 99 | 97 | 86 | 92 | 98 | 92 | 94 |
| 87 | 89 | 99 | 92 | 99 | 92 | 93 | 76 | 70 | 90 | 92 | 64 |
(2)补全下面的茎叶图,并求样本的众数和极差;
(3)在对数据进一步分析时,满足|x-96.5|≤4的预考成绩,称为具有M特性.在样本中随机抽取一人,
求此人的预考成绩具有M特性的概率.
考点:茎叶图,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)求出A、B、C三个驾校的总人数,根据同一比例求出从三个驾校分别应抽的人数;
(2)根据表中数据,补全茎叶图,求出样本的众数与极差;
(3)求出满足|x-96.5|≤4的预考成绩的个数,计算满足条件的概率.
(2)根据表中数据,补全茎叶图,求出样本的众数与极差;
(3)求出满足|x-96.5|≤4的预考成绩的个数,计算满足条件的概率.
解答:
解:(1)∵A、B、C三个驾校的人数分别是150、200、250,
∴从三个驾校分别应抽的人数是24×
=6,
24×
=8,
24×
=10;
(2)根据表中数据,补全茎叶图如图所示,
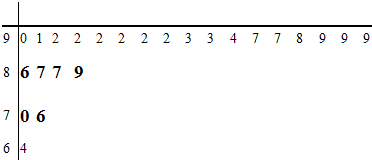
根据茎叶图,得;
样本的众数是92,
极差是99-64=35;
(3)根据题意,满足|x-96.5|≤4的预考成绩,有99、99、99、98、97、97、94、93、93共9个,
在样本数据中随机抽取一人,则此人的预考成绩具有M特性的概率是P=
=
.
∴从三个驾校分别应抽的人数是24×
| 150 |
| 150+200+250 |
24×
| 200 |
| 150+200+250 |
24×
| 250 |
| 150+200+250 |
(2)根据表中数据,补全茎叶图如图所示,
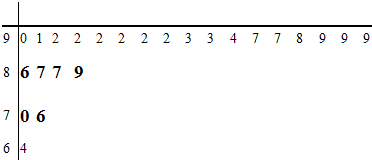
根据茎叶图,得;
样本的众数是92,
极差是99-64=35;
(3)根据题意,满足|x-96.5|≤4的预考成绩,有99、99、99、98、97、97、94、93、93共9个,
在样本数据中随机抽取一人,则此人的预考成绩具有M特性的概率是P=
| 9 |
| 24 |
| 3 |
| 8 |
点评:本题考查了茎叶图的应用问题,考查了求众数与极差,以及求概率的问题,是基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
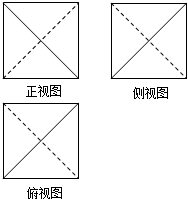 某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )A、
| ||||
| B、3π | ||||
| C、π | ||||
D、
|
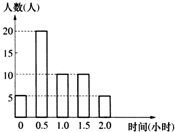 某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为
某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为