Question

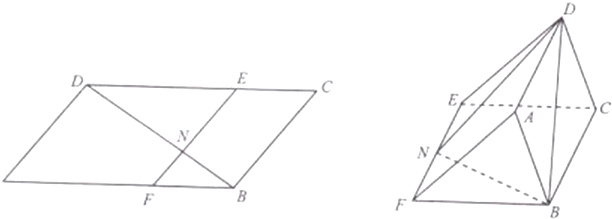
如图，已知ABCD为平行四边形，∠A=60°，AB=6，点E在CD上，BD⊥AD，BD交EF于点N，且

AF

FB

+

DN

NB

+

DE

EC

=2，现将四边形ADEF沿EF折起，使点D在平面BCEF上的射影恰在B处．
（1）求证：BN⊥CD
（2）试问在直线DN上是否存在点G，使BG∥平面EDC，若存在，求出直线CG与平面EDC所成的正弦值，若不存在，请说明理由．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的性质

专题：空间角

分析：（1）根据线面垂直的性质证明BN⊥平面ABCD，即可证明BN⊥CD
（2）建立空间直角坐标系，利用向量法即可得到结论．

解答： 证明：（1）∵点D在平面BCEF上的射影恰好在点B处，
∴BD⊥BN，又BN⊥BC，
于是BN⊥平面ABCD，而CD?平面ABCD，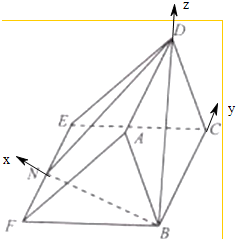
故BN⊥CD
（2）分别以BN，BC，BD所在的直线为x，y，z轴，建立空间直角坐标系，
由题可得N（

3

，0，0），D（0，0，3），C（0，3，0），E（

3

，2，0），
设平面EDC的法向量为

m

=（x，y，z），
则

DE

=（

3

，2，-3），

DC

=（0，3，-3），
由

m • DE =0 m • DC =0

，即

3 x+2y-3z=0 3y-3z=0

，令x=1，则y=z=

3

，
即

m

=（1，

3

，

3

），

DN

=(

3

，0，-3)，
假设存在点G，使BG∥平面EDC，设G（x，y，z），
则

DG

=(x，y，z-3)，
∵

DG

∥

DN

，
∴y=0，z=3-

3

x，

BC

=(x，0，3-

3

x)，
∵BG∥平面EDC，
∴

BG

⊥

m

，
即

BG

•

m

=0，解得x=

3 3

2

，即存在G（

3 3

2

，0，-

3

2

），使BG∥平面EDC，

CG

=(

3 3

2

，-3，-

3

2

)，
则cos＜

CG

，

m

＞=

CG • m

| CG |•| m |

=-

42

14

，
∴直线CG与平面EDC所成的正弦值为

42

14

．

点评：本题主要考查空间线面垂直的判定，以及直线和平面所成角的求解，利用向量法是解决本题的关键．