Question

【题目】已知函数， （为常数）.

(Ⅰ) 函数的图象在点处的切线与函数的图象相切，求实数的值；

(Ⅱ) 若， ，且，都有成立，求实数的值.

Answer 1

【答案】（Ⅰ）；（Ⅱ） .

【解析】试题分析：（Ⅰ）利用导数求出函数的图象在点处的切线方程，再由直线与函数的图象相切的关系，联立方程组求出的值；(Ⅱ)依题意不妨设，根据对数函数及二次函数的性质可判断及的单调性，可把等价转化为，等价于，再构造函数，即等价于 在区间上是增函数，利用导数与函数单调性的关系，结合不等式恒成立的条件，即可求得实数的值.

试题解析：（Ⅰ）∵

∴，则

∴函数的图象在点处的切线方程为，

由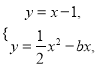得.

由，得.（还可以通过导数来求）

(Ⅱ)不妨设，

∵函数在区间上是增函数，

∴，

∵函数图象的对称轴为，且.

∴当时，函数在区间上是减函数，

∴，

∴，

等价于，

即，

等价于 在区间上是增函数，

等价于在区间上恒成立，

等价于在区间上恒成立

∴

又∵

∴

点睛: 本题主要考查导数的应用,包括导数的几何意义,导数与单调性,属于中档题.本题在第2问中注意解题思想:等价转换,将原不等式转化为求在上为增函数,等价于在区间上恒成立,分离出,转化为求在上的最小值.