题目内容
设Sn是等比数列{an}的前n项和,若2a1+3a2=1,a3=3a4,则2Sn+an= .
【答案】分析:先根据2a1+3a2=1,a3=3a4求得q以及首项,进而得到其通项以及其前n项和的表达式,即可求出答案.
解答:解:设公比为q,
∵2a1+3a2=1,a3=3a4,
∴2a1+3a1q=1;①
a1q2=3a1q3;②
由②得q= ,代入①得a1=
,代入①得a1= ;
;
∴an=a1•qn-1=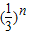 ;
;
sn=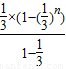 =
= (1-
(1-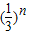 ).
).
∴2Sn+an=1-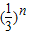 +
+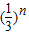 =1.
=1.
故答案为:1.
点评:本题主要考查等比数列的求和公式的应用.解决本题的关键在于熟练掌握等比数列的通项公式以及求和公式.
解答:解:设公比为q,
∵2a1+3a2=1,a3=3a4,
∴2a1+3a1q=1;①
a1q2=3a1q3;②
由②得q=
 ,代入①得a1=
,代入①得a1= ;
;∴an=a1•qn-1=
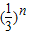 ;
;sn=
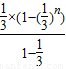 =
= (1-
(1-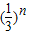 ).
).∴2Sn+an=1-
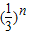 +
+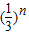 =1.
=1.故答案为:1.
点评:本题主要考查等比数列的求和公式的应用.解决本题的关键在于熟练掌握等比数列的通项公式以及求和公式.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
设Sn是等比数列{an}的前n项和,
=
,则
等于( )
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 的前n项和,若
的前n项和,若 ,则
,则 ( )
( )  B、
B、 C、
C、 D、
D、
 ,则
,则 等于( )
等于( )



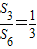 ,则
,则 等于( )
等于( )


