题目内容
设Sn是等比数列{an}前n项的乘积,若a9=1,则下面的等式中正确的是( )
分析:先确定数列首项与公比的关系,求出等比数列{an}前n项的乘积的表达式,代入验证,即可得到结论.
解答:解:设等比数列{an}的首项为a1,公比为q,则a1q8=1
∵Sn是等比数列{an}前n项的乘积,
∴Sn=(a1)nq1+2+…+(n-1)=(a1q
)n
∴S5=(a1q
)5=q-30,S12=(a1q
)12=q-30
∴S5=S12,
故选C.
∵Sn是等比数列{an}前n项的乘积,
∴Sn=(a1)nq1+2+…+(n-1)=(a1q
| n-1 |
| 2 |
∴S5=(a1q
| 5-1 |
| 2 |
| 12-1 |
| 2 |
∴S5=S12,
故选C.
点评:本题考查等比数列的通项,考查等比数列{an}前n项的乘积,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
设Sn是等比数列{an}的前n项和,
=
,则
等于( )
| S3 |
| S6 |
| 1 |
| 3 |
| S6 |
| S12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 的前n项和,若
的前n项和,若 ,则
,则 ( )
( )  B、
B、 C、
C、 D、
D、
 ,则
,则 等于( )
等于( )



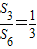 ,则
,则 等于( )
等于( )


