题目内容
已知定点A(1,0)和直线x=-1上的两个动点E,F,且(1)求动点P的轨迹C的方程;
(2)已知点B(a,0),过点B的直线与轨迹C交于两个不同的点M,N,若∠MON为锐角,求实数a的取值范围。
解:(1)设P(x,y),则由已知得E(-1,y),![]() =(-2,y),设F(-1,b,),则
=(-2,y),设F(-1,b,),则![]() =(-2,b),
=(-2,b), ![]() =(1,-b),
=(1,-b),
∵![]() ,∴4+yb=0
,∴4+yb=0![]() yb=-4,由
yb=-4,由![]() ∥
∥![]()
![]() y+bx=0,
y+bx=0,
∴所求轨迹方程为y2=4x(x≠0).
(2)设过点B(a,0)的直线方程为x=ty+a,
代入方程y2=4x中得:y2-4ty-4a=0,设M(x1,y1),N(x2,y2),则y1y2=-4a.
∵∠MON是锐角,则![]() >0,即x1x2+y1y2=
>0,即x1x2+y1y2=![]() =a2-4a>0,
=a2-4a>0,
所以a>4或a<0

练习册系列答案
相关题目
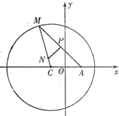 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足