Question

17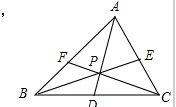．P为△ABC内一点，AP，BP，CP分别交对边于D，E，F．已知AP=BP=CP=6，设PD=x，PE=y，PF=z，xy+yz+zx=28，则xyz=24．

Answer 1

分析 利用面积关系，确定$\frac{3}{x+6}+\frac{3}{y+6}+\frac{3}{z+6}$=1，即可求出xyz．

解答 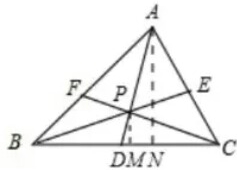解：如图，作PM⊥BC，AN⊥BC，垂足分别为M，N，则
$\frac{{S}_{△PBC}}{{S}_{△ABC}}$=$\frac{x}{x+6}$，$\frac{{S}_{△PAC}}{{S}_{△ABC}}$=$\frac{y}{y+6}$，$\frac{{S}_{△PAB}}{{S}_{△ABC}}$=$\frac{z}{z+6}$，
∴$\frac{x}{x+6}$+$\frac{y}{y+6}$+$\frac{z}{z+6}$=1
∴$\frac{3}{x+6}+\frac{3}{y+6}+\frac{3}{z+6}$=1，
∴3（yz+zx+xy）+36（x+y+z）+324=xyz+6（xy+yz+zx）+36（x+y+z）+216，
∵xy+yz+zx=28，
∴xyz=108-3（xy+yz+zx）=24．
故答案为：24．

点评 本题考查三角形面积的计算，考查学生分析解决问题的能力，确定$\frac{3}{x+6}+\frac{3}{y+6}+\frac{3}{z+6}$=1是关键．