题目内容
6．比较大小：$\frac{1}{\sqrt{n+1}-\sqrt{n}}$＞2$\sqrt{n}$（填“≥”“≤”或“＜”）．分析 先进行分母有理化即可比较大小．
解答 解：$\frac{1}{\sqrt{n+1}-\sqrt{n}}$=$\sqrt{n+1}$+$\sqrt{n}$＞$\sqrt{n}$+$\sqrt{n}$＞2$\sqrt{n}$
∴$\frac{1}{\sqrt{n+1}-\sqrt{n}}$＞2$\sqrt{n}$，
故答案为：＞
点评 本题考查了不等式大小比较的方法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
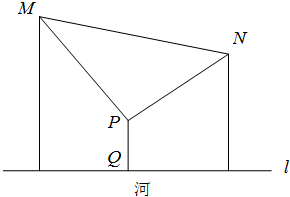如图，相距14km的两个居民小区M和N位于河岸l（直线）的同侧，M和N距离河岸分别为10km和8km．现要在河的小区一侧选一地点P，在P处建一个生活污水处理站，从P排直线水管PM，PN分别到两个小区和垂直于河岸的水管PQ，使小区污水经处理后排入河道．设PQ段长为t km（0＜t＜8）．
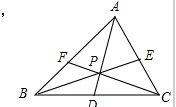P为△ABC内一点，AP，BP，CP分别交对边于D，E，F．已知AP=BP=CP=6，设PD=x，PE=y，PF=z，xy+yz+zx=28，则xyz=24．
1．设M=${∫}_{1}^{2}$log${\;}_{\frac{1}{2}}$xdx，N=${∫}_{1}^{2}$log${\;}_{\frac{1}{3}}$xdx，则（ ）
| A． | M＞N | B． | M＜N | C． | |M|＜|N| | D． | |M|=|N| |