题目内容
5.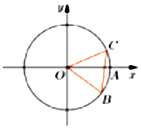 如图,圆O与x轴正半轴交点为A,点B,C在圆O上,圆C在第一象限,且B($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=-$\frac{3}{5}$.
如图,圆O与x轴正半轴交点为A,点B,C在圆O上,圆C在第一象限,且B($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=-$\frac{3}{5}$.
分析 由题意求得∠AOB=$\frac{π}{3}$-α,由直角三角形中的三角函数的定义可得sin($\frac{π}{3}$-α)=sin∠AOB=$\frac{3}{5}$,利用诱导公式化简可求cos($\frac{5π}{6}$-α)的值.
解答 解:如图,由B($\frac{4}{5}$,-$\frac{3}{5}$),得OB=OC=1,又BC=1,
∴∠BOC=$\frac{π}{3}$,∠AOB=$\frac{π}{3}$-α,由直角三角形中的三角函数的定义可得sin($\frac{π}{3}$-α)=sin∠AOB=$\frac{3}{5}$,
∴cos($\frac{5π}{6}$-α)=cos[($\frac{π}{3}$-α)+$\frac{π}{2}$]=-sin($\frac{π}{3}$-α)=-$\frac{3}{5}$.
故答案为:-$\frac{3}{5}$.
点评 本题考查三角函数的化简求值,考查三角函数的定义,考查诱导公式在三角函数化简求值中的应用,是基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
15.已知集合A={0,1,2,3,4},集合B={x|x=2n,n∈A},则A∩B=( )
| A. | {0} | B. | {0,2,4} | C. | {2,4} | D. | {0,2} |
16.设D、E、F分别为△ABC三边BC、CA、AB的中点,则$\overrightarrow{DA}$+2$\overrightarrow{EB}$+3$\overrightarrow{FC}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{3}{2}$$\overrightarrow{AD}$ | C. | $\frac{1}{2}$$\overrightarrow{AC}$ | D. | $\frac{3}{2}$$\overrightarrow{AC}$ |
13.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆x2+y2=$\frac{{b}^{2}}{4}$的切线,切点为E,延长FE交双曲线C的右支于点P,若E为PF的中点,则双曲线C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\frac{\sqrt{5}+1}{2}$ |
20.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{2π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=4,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
10.已知集合A={x|2x-1<0},B={x|0≤x≤1},那么A∩B等于( )
| A. | {x|x≥0} | B. | {x|x≤1} | C. | $\left\{{\left.x\right|0<x≤\frac{1}{2}}\right\}$ | D. | {x|0≤x<$\frac{1}{2}$} |
15.某公司在2012-2016年的收入与支出情况如表所示:
根据表中数据可得回归直线方程为$\widehat{y}$=0.8x+$\widehat{a}$,依次估计如果2017年该公司收入为7亿元时的支出为( )
| 收入x(亿元) | 2.2 | 2.6 | 4.0 | 5.3 | 5.9 |
| 支出y(亿元) | 0.2 | 1.5 | 2.0 | 2.5 | 3.8 |
| A. | 4.5亿元 | B. | 4.4亿元 | C. | 4.3亿元 | D. | 4.2亿元 |