题目内容
14．若正实数x、y满足x+y+$\frac{1}{x}$+$\frac{1}{y}$=5，则x+y的最大值与最小值的和为5．分析 由题意可得，（x+y）[5-（x+y）]=（x+y）（$\frac{1}{x}$+$\frac{1}{y}$）=2+$\frac{y}{x}$+$\frac{x}{y}$，利用基本不等式即可得出最值，进而得到它们的和．
解答 解：∵x+y+$\frac{1}{x}$+$\frac{1}{y}$=5，
∴（x+y）[5-（x+y）]=（x+y）（$\frac{1}{x}$+$\frac{1}{y}$）=2+$\frac{y}{x}$+$\frac{x}{y}$≥2+2$\sqrt{\frac{y}{x}•\frac{x}{y}}$=4，
∴（x+y）2-5（x+y）+4≤0，
∴1≤x+y≤4，
∴当且仅当x=y=2时，x+y取最大值4，x=y=$\frac{1}{2}$时，x+y取得最小值为1，
则x+y的最大值与最小值的和为5．
故答案为：5．
点评 本题考查最值求法，注意运用变形和基本不等式，考查运算能力，属于中档题．
练习册系列答案
相关题目
，则
”的否命题是 .
，
，则函数
在区间
上的零点个数为 ．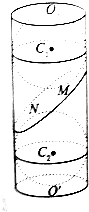
如图，已知圆柱OO′的底面半径为12，与底面成β角（其中cosβ=$\frac{12}{13}$，sinβ=$\frac{5}{13}$）的截面α截圆柱所得的平面图形为椭圆，已知球C1，C2分别与圆柱的侧面、底面相切，与截面α相切于点M、N，在圆柱OO′的体积为（ ）
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，左、右焦点分别是F1、F2，以原点O为圆心，椭圆C的短半轴为半径的圆与直线l：x-y+2=0相切．