题目内容
8.已知△ABC的内角A,B,C所对的边分别为a,b,c,若B=$\frac{π}{3}$,b=4,则△ABC的面积的最大值为4$\sqrt{3}$.分析 通过余弦定理以及基本不等式求出ac的最大值,然后求解三角形的面积的最大值.
解答 解:△ABC的内角A,B,C所对的边分别为a,b,c,若B=$\frac{π}{3}$,b=4,
可得:16=b2=a2+c2-2accos$\frac{π}{3}$=a2+c2-ac≥2ac-ac=ac,当且仅当a=c=4时等号成立.
∴${S_{△ABC}}=\frac{1}{2}acsinB≤\frac{1}{2}×16×\frac{{\sqrt{3}}}{2}=4\sqrt{3}$,
当且仅当a=c=4时,${({S_{△ABC}})_{max}}=4\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查余弦定理的应用,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
19.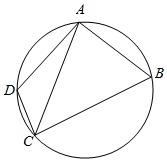 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
13.执行如图所示的程序框图,若输出的n的值为7,则输入的T的最大值为( )


| A. | 339 | B. | 212 | C. | 190 | D. | 108 |
20.已知全集U=R,集合A={x|(x+2)(x-2)≤0},则集合∁RA=( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2]∪[2,+∞) |
17.已知等比数列{an}单调递减,满足a1a5=9,a2+a4=10,则数列{an}的公比q=( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 3 |
18.已知z是纯虚数,i为虚数单位,$\frac{z+2}{1-i}$在复平面内所对应的点在实轴上,那么z等于( )
| A. | 2i | B. | i | C. | -i | D. | -2i |
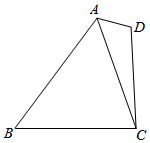 如图,在四边形ABCD中,AB=4,AC=2$\sqrt{3}$,cos∠ACB=$\frac{1}{3}$,∠D=2∠B.
如图,在四边形ABCD中,AB=4,AC=2$\sqrt{3}$,cos∠ACB=$\frac{1}{3}$,∠D=2∠B.