题目内容
设A、B分别是直线y=(1)求轨迹C的方程;
(2)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且DM=λDN(λ≠1),求实数λ的取值范围.
解:(1)设P(x,y),∵A、B分别为直线y=![]() x和y=-
x和y=-![]() x上的点,故可设A(x1,
x上的点,故可设A(x1,![]() x1)、B(x2,-
x1)、B(x2,-![]() x2).∵
x2).∵![]() =
=![]() +
+![]() ,∴
,∴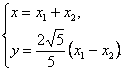 ∴
∴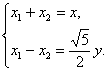
?
又|![]() |=
|=![]() ,∴(x1-x2)2+
,∴(x1-x2)2+![]() (x1+x2)2=20. ?
(x1+x2)2=20. ?
∴![]() y2+
y2+![]() x2=20,即曲线C的方程为
x2=20,即曲线C的方程为![]() ?
?
(2)设N(s,T)、M(x,y),则由![]() ,可得(x,y-16)=λ(s,T-16).?
,可得(x,y-16)=λ(s,T-16).?
故x=λs,y=16+λ(T-16). ?
∵M、N在曲线C上,∴ ?
?
消去s得![]() .?
.?
由题意知λ≠0且λ≠1,解得T=![]() . ?
. ?
又|T|≤4,∴|![]() |≤4.解之,得
|≤4.解之,得![]() ≤λ≤
≤λ≤![]() (λ≠1).?
(λ≠1).?
故实数λ的取值范围是![]() ≤λ≤
≤λ≤![]() (λ≠1).
(λ≠1).

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目