题目内容
在△ABC中,若a=4,b=3,cosA=
,则B=( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理
专题:解三角形
分析:cosA=
,A∈(0,π),可得sinA=
,由正弦定理可得:
=
,即可得出sinB.而a>b,可得A>B.即可得出.
| 1 |
| 3 |
| 1-cos2A |
| a |
| sinA |
| b |
| sinB |
解答:
解:∵cosA=
,A∈(0,π),
∴sinA=
=
.
由正弦定理可得:
=
,
∴sinB=
=
=
.
∵a>b,
∴A>B.
∴B为锐角,∴B=
.
故选:A.
| 1 |
| 3 |
∴sinA=
| 1-cos2A |
2
| ||
| 3 |
由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
∴sinB=
| bsinA |
| a |
3×
| ||||
| 4 |
| ||
| 2 |
∵a>b,
∴A>B.
∴B为锐角,∴B=
| π |
| 4 |
故选:A.
点评:本题考查了正弦定理的应用、同角三角函数基本关系式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
在区域
内任取一点P,则点P落在单位圆x2+y2=1内的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
某几何体的三视图如图实数,则当x+y取最大值时,该几何体的体积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
阅读程序框图,若m、n分别是双曲线
-
=1的虚轴长和实半轴长,则输出a,i别是( ) 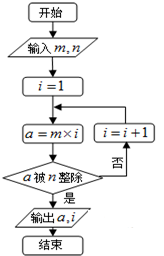
| x2 |
| 36 |
| y2 |
| 4 |

| A、a=12,i=3 |
| B、a=12,i=4 |
| C、a=8,i=3 |
| D、a=8,i=4 |
函数f(x)=2x2-3x+1的零点个数是( )
| A、0 | B、1 | C、2 | D、3 |

