Question

某几何体的三视图如图实数，则当x+y取最大值时，该几何体的体积为（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  1

  6

• D、

  2

  3

Answer 1

考点：由三视图求面积、体积

专题：计算题,空间位置关系与距离

分析：该几何体是长方体一角，作出图形，确定x+y≤4，再求当x+y取最大值时，该几何体的体积．

解答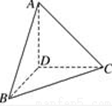： 解：该几何体是长方体一角，如图所示，可知AC=

6

，BD=1，BC=y，AB=x．设CD=a，AD=b，
则a²+b²=6，a²+1=y²，b²+1=x²，
消去a²，b²得x²+y²=8≥

(x+y)2

2

，所以x+y≤4，
当且仅当x=y=2时等号成立，此时a=b=

3

，
所以V=

1

3

×

1

2

×1×

3

×

3

=

1

2

．
故选A．

点评：本题主要考查三视图，几何体体积计算，均值定理的应用．