题目内容
17.已知向量$\overrightarrow a=(\sqrt{3}sin2x+3,cosx)$,$\overrightarrow b=(1,2cosx)$,设函数$f(x)=\overrightarrow a•\overrightarrow b$(1)求函数f(x)的最小正周期和其图象的对称中心;
(2)当$x∈[\frac{π}{12},\frac{7π}{12}]$时,求函数f(x)的值域.
分析 (1)进行数量积的坐标运算,并化简即可求得$f(x)=2sin(2x+\frac{π}{6})+4$,进而求出f(x)的最小正周期及对称中心;
(2)根据x的范围便可求出$2x+\frac{π}{6}$的范围,根据f(x)的解析式即可求出f(x)的值域.
解答 解:(1)$f(x)=\overrightarrow{a}•\overrightarrow{b}$
=$\sqrt{3}sin2x+3+2co{s}^{2}x$
=$\sqrt{3}sin2x+cos2x+4$
=$2sin(2x+\frac{π}{6})+4$;
∴f(x)的周期T=π;
令$2x+\frac{π}{6}=kπ$,k∈Z,则x=$\frac{kπ}{2}-\frac{π}{12}$,k∈Z;
∴图象对称中心为:$(\frac{kπ}{2}-\frac{π}{12},4)$,k∈Z;
(2)$f(x)=2sin(2x+\frac{π}{6})+4$;
$x∈[\frac{π}{12},\frac{7π}{12}]$,∴$2x+\frac{π}{6}∈[\frac{π}{3},\frac{4π}{3}]$;
∴f(x)∈[3,6];
即f(x)的值域为[3,6].
点评 考查数量积的坐标运算,二倍角的余弦公式,两角和的正弦公式,周期的计算公式,正弦函数的对称中心,以及正弦函数的图象.

练习册系列答案
相关题目
13.-390°角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
5.设△ABC的内角A,B,C所对的边分别是a,b,c,设向量$\overrightarrow{m}$=(a,b),$\overrightarrow{n}$=(sinB,sinA),若$\overrightarrow{m}$∥$\overrightarrow{n}$,则△ABC为( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等腰三角形 | D. | 无法确定 |
12.设x,y∈R命题p:x>1且y>1,q:x+y>2,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.在扇形AOB中,∠AOB=$\frac{5π}{6}$,C在弧AB上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x与y满足关系式( )
| A. | x2-$\sqrt{3}$xy+y2=1 | B. | x2-xy+y2=1 | C. | x2+y2=1 | D. | x2+xy+y2=1 |
9.在等差数列{an}中,a4=5,则a3+a5=( )
| A. | 20 | B. | 12 | C. | 10 | D. | 36 |
6.函数f(x)的导函数f'(x),满足关系式f(x)=x2+2xf'(2)-lnx,则f'(2)的值为( )
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
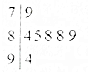 某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )
某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )