题目内容
2.在扇形AOB中,∠AOB=$\frac{5π}{6}$,C在弧AB上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x与y满足关系式( )| A. | x2-$\sqrt{3}$xy+y2=1 | B. | x2-xy+y2=1 | C. | x2+y2=1 | D. | x2+xy+y2=1 |
分析 建立如图所示的直角坐标系,不妨设r=1.A(1,0),B$(-\frac{\sqrt{3}}{2},\frac{1}{2})$.设C(m,n),$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,可得$\left\{\begin{array}{l}{m=x-\frac{\sqrt{3}}{2}y}\\{n=\frac{1}{2}y}\end{array}\right.$,即可得出.
解答 解:建立如图所示的直角坐标系,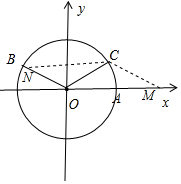
不妨设r=1.
A(1,0),B$(-\frac{\sqrt{3}}{2},\frac{1}{2})$.
设C(m,n),$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则$\left\{\begin{array}{l}{m=x-\frac{\sqrt{3}}{2}y}\\{n=\frac{1}{2}y}\end{array}\right.$,
则m2+n2=$(x-\frac{\sqrt{3}}{2}y)^{2}$+$(\frac{1}{2}y)^{2}$=1,
化为:x2-$\sqrt{3}$xy+y2=1.
故选:A.
点评 本题考查了平面向量基本定理、圆的方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{-\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | (-∞,$\frac{1}{4}$) | B. | (2,+∞) | C. | (-2,$\frac{1}{4}$) | D. | (-∞,2)∪($\frac{1}{4}$,+∞) |
11.椭圆$\frac{x^2}{m}+\frac{y^2}{4}=1$的焦距为$2\sqrt{2}$,则m的值等于( )
| A. | 5或-3 | B. | 2或6 | C. | 5或3 | D. | $\sqrt{5}$或$\sqrt{3}$ |