题目内容
解关于x的不等式
(1)
≤2;
(2)x2-ax-2a2<0.
(1)
| 3x-5 |
| x2+2x-3 |
(2)x2-ax-2a2<0.
考点:其他不等式的解法
专题:不等式的解法及应用
分析:(1)不等式即
≥0,再用穿根法求得它的解集.
(2)不等式即 (x+a)(x-2a)<0,分当a=0时、当a>0时、当a<0时三种情况,分别求得不等式的解集.
| (2x-1)(x+1) |
| (x+3)(x-1) |
(2)不等式即 (x+a)(x-2a)<0,分当a=0时、当a>0时、当a<0时三种情况,分别求得不等式的解集.
解答:
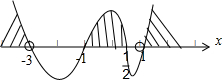 解:(1)不等式
解:(1)不等式
≤2,即
≥0,
即
≥0,
用穿根法求得它的解集为 {x|x<-3,或-1≤x≤
,或x>1}.
(2)x2-ax-2a2<0,即 (x+a)(x-2a)<0,
当a=0时,不等式的解集为∅;
当a>0时,不等式的解集为{x|-a<x<2a};
当a<0时,不等式的解集为{x|2a<x<-a}.
 解:(1)不等式
解:(1)不等式 | 3x-5 |
| x2+2x-3 |
| 2x2+x-1 |
| x2+2x-3 |
即
| (2x-1)(x+1) |
| (x+3)(x-1) |
用穿根法求得它的解集为 {x|x<-3,或-1≤x≤
| 1 |
| 2 |
(2)x2-ax-2a2<0,即 (x+a)(x-2a)<0,
当a=0时,不等式的解集为∅;
当a>0时,不等式的解集为{x|-a<x<2a};
当a<0时,不等式的解集为{x|2a<x<-a}.
点评:本题主要考查分式不等式、一元二次不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设Q是曲线T:xy=1(x>0)上任意一点,l是曲线T在点Q处的切线,且l交坐标轴于A,B两点,则△OAB的面积(O为坐标原点)( )
| A、为定值2 |
| B、最小值为3 |
| C、最大值为4 |
| D、与点Q的位置有关 |
 在正四面体ABCD中,M,N分别是BC,AD中点.
在正四面体ABCD中,M,N分别是BC,AD中点.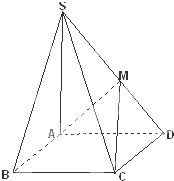 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB.

 已知函数y=
已知函数y=