题目内容
1.已知f(x)=$\frac{bx+1}{(ax+1)^{2}}$(x≠-$\frac{1}{a}$,a>0),且f(1)=log162,f(-2)=1.(1)求函数f(x)的表达式;
(2)已知数列{xn}的项满足xn=[1-f(1)][1-f(2)]…[1-f(n)],试求x1,x2,x3,x4;
(3)猜想{xn}的通项公式.(不需要证明)
分析 (1)把f(1)=log162=$\frac{1}{4}$,f(-2)=1,代入函数表达式得:$\frac{b+1}{(a+1)^{2}}$=$\frac{1}{4}$,$\frac{-2b+1}{(-2a+1)^{2}}$=1,解得a,b.
(2)x1=1-f(1)=1-$\frac{1}{4}$=$\frac{3}{4}$,同理可得x2,x3,x4.
(3)由(2)知,x1=$\frac{3}{4}$,x2=$\frac{2}{3}$=$\frac{4}{6}$,x3=$\frac{5}{8}$,x4=$\frac{3}{5}$=$\frac{6}{10}$,…,由此可以猜想xn.
解答 解:(1)把f(1)=log162=$\frac{1}{4}$,f(-2)=1,代入函数表达式得:$\frac{b+1}{(a+1)^{2}}$=$\frac{1}{4}$,$\frac{-2b+1}{(-2a+1)^{2}}$=1,
解得:a=1,b=0,(舍去a=-$\frac{1}{3}$<0),
∴f(x)=$\frac{1}{(x+1)^{2}}$(x≠-1).
(2)x1=1-f(1)=1-$\frac{1}{4}$=$\frac{3}{4}$,
x2=[1-f(1)][1-f(2)]=$\frac{3}{4}$×(1-$\frac{1}{9}$)=$\frac{2}{3}$,
x3=$\frac{2}{3}$[1-f(3)]=$\frac{2}{3}$×(1-$\frac{1}{16}$)=$\frac{5}{8}$,
x4=$\frac{5}{8}$×(1-$\frac{1}{25}$)=$\frac{3}{5}$.
(3)由(2)知,x1=$\frac{3}{4}$,x2=$\frac{2}{3}$=$\frac{4}{6}$,x3=$\frac{5}{8}$,x4=$\frac{3}{5}$=$\frac{6}{10}$,…,由此可以猜想xn=$\frac{n+2}{2n+2}$.
点评 本题考查了对数函数的运算法则、方程的解法、数列通项公式,考查了推理能力与计算能力,属于中档题.

| A. | {-2} | B. | {-1,0} | C. | {-1,0,1} | D. | {-2,-1,0,1} |
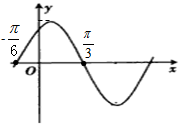 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$或-2 | C. | $\frac{1}{2}$或2 | D. | -2 |