题目内容
8. 在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=$\frac{1}{2}$CD.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=$\frac{1}{2}$CD.(Ⅰ)求证:面PAD⊥面PAC;
(Ⅱ)若AB=1,求三棱锥D-PBC的高.
分析 (Ⅰ)设PA=AB=BC=$\frac{1}{2}$CD=a,通过求解直角三角形可得AD2+AC2=CD2,得到AC⊥AD.由PA⊥底面ABCD,得PA⊥AC,再由线面垂直的判定可得AC⊥平面PAD,从而得到平面PAD⊥平面PAC;
(Ⅱ)设三棱锥D-PBC的高为h,利用VD-PBC=VP-DBC求得三棱锥D-PBC的高h.
解答 (Ⅰ)证明:设PA=AB=BC=$\frac{1}{2}$CD=a,在Rt△ABC中,AC=$\sqrt{2}$a,
在直角梯形ABCD中 ,求得AD=$\sqrt{2}$a,
,求得AD=$\sqrt{2}$a,
在△DAC中,有AD2+AC2=CD2,∴AC⊥AD.
又∵PA⊥底面ABCD,∴PA⊥AC,
又PA∩AD=A,∴AC⊥平面PAD,
∵AC?平面PAC,∴平面PAD⊥平面PAC;
(Ⅱ)解:设三棱锥D-PBC的高为h,由题知PA=AB=BC=1,DC=2,PB=$\sqrt{2}$.
∵BC⊥AB,PA⊥BC,PA∩AB=A,∴BC⊥平面PAB,则BC⊥PB.
∵VD-PBC=VP-DBC,
∴$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×1×h$=$\frac{1}{3}×\frac{1}{2}×2×1×1$,解得h=$\sqrt{2}$,
∴三棱锥D-PBC的高为$\sqrt{2}$.
点评 本题考查线面垂直的判定,考查面面垂直的判定,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
16.已知函数f(x)=$\frac{x+a}{{x}^{2}+b}$的图象在点M(-1,f(-1))处的切线方程为x-4y+1=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的极值.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的极值.
20.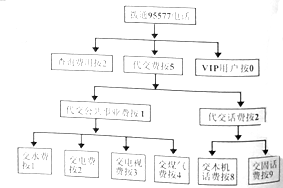 某银行推出95577服务电话,部分业务流程如图,如果我要利用这个服务交纳电视费,请问按照这个流程图,我拨通95577电话后如何操作( )
某银行推出95577服务电话,部分业务流程如图,如果我要利用这个服务交纳电视费,请问按照这个流程图,我拨通95577电话后如何操作( )
 某银行推出95577服务电话,部分业务流程如图,如果我要利用这个服务交纳电视费,请问按照这个流程图,我拨通95577电话后如何操作( )
某银行推出95577服务电话,部分业务流程如图,如果我要利用这个服务交纳电视费,请问按照这个流程图,我拨通95577电话后如何操作( )| A. | 按2,按1,按3 | B. | 按5,按1,按3 | C. | 按0,按2,按1,按3 | D. | 按5,按1,按2 |
 如图是一几何体的直观图、主视图和俯视图,则该几何体的侧视图是( )
如图是一几何体的直观图、主视图和俯视图,则该几何体的侧视图是( )



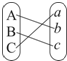 连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;
连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;