题目内容
17．设二项式（x-$\frac{a}{x}$）6的展开式中x2项的系数为A，常数项为B，若B=4A，则非零实数a的值为-3．分析 利用二项展开式的通项公式，求得A和B，再根据B=4A，求得a的值．
解答 解：∵二项式（x-$\frac{a}{x}$）6的展开式的通项公式为Tr+1=${C}_{6}^{r}$•（-a）r•x6-2r，
令6-2r=2，可得 r=2，故展开式中x2项的系数为A=${C}_{6}^{2}$•a2，
令6-2r=0，求得r=3，可得常数项为B=${C}_{6}^{3}$•（-a）3，
若B=4A，则${C}_{6}^{3}$•（-a）3=4${C}_{6}^{4}$•a2，a=-3，
故答案为：-3．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=$\frac{1}{2}$．则下列结论中正确的个数为（ ）
在四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AB⊥BC，PA=AB=BC=$\frac{1}{2}$CD．
5．函数f（x）=sinxcosx-$\frac{\sqrt{3}}{2}$cos2x，则f（$\frac{π}{24}$）=（ ）
| A． | -$\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
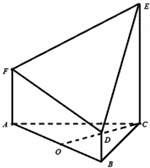如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得，已知FA⊥平面ABC，AB=2，BD=1，AF=2，CE=3，O为AB的中点．
已知在长方体ABCD-A1B1C1D1中，E、M、N分别是BC、AE、D1C的中点，AD=AA1，AB=2AD