��Ŀ����
���壺max{x��y}��ʾx��y�������е����ֵ��min{x��y}��ʾx��y�������е���Сֵ����������4�����⣺
��max{x1��x2}��a?x1��a��x2��a��
��max{x1��x2}��a?x1��a��x2��a��
���躯��f��x����g��x���Ĺ���������ΪD����x��D��f��x����g��x�����������[f��x��]min��[g��x��]max��
��������f��x��=min{|x|��|x+t|}��ͼ�����ֱ��x=-
�Գƣ���t��ֵΪ1��
������������ ����д���������������ţ�
��max{x1��x2}��a?x1��a��x2��a��
��max{x1��x2}��a?x1��a��x2��a��
���躯��f��x����g��x���Ĺ���������ΪD����x��D��f��x����g��x�����������[f��x��]min��[g��x��]max��
��������f��x��=min{|x|��|x+t|}��ͼ�����ֱ��x=-
| 1 |
| 2 |
������������
���㣺���������ж���Ӧ��
ר�⣺�ۺ���,���������ʼ�Ӧ��
�������٣���max{x1��x2}��a?x1��a��x2��a�����жϢ٣�
�ڣ���max{x1��x2}��a֪x1��a��x2��a�����жϢڣ�
�ۣ������⣬��x��D��f��x����g��x�����������[f��x��]min��[g��x��]max�����жϢۣ�
�ܣ���������f��x��=min{|x|��|x+t|}����ֱ��x=-
�ԳƵ�ͼ�����t��ֵ�����жϢܣ�
�ڣ���max{x1��x2}��a֪x1��a��x2��a�����жϢڣ�
�ۣ������⣬��x��D��f��x����g��x�����������[f��x��]min��[g��x��]max�����жϢۣ�
�ܣ���������f��x��=min{|x|��|x+t|}����ֱ��x=-
| 1 |
| 2 |
���
�⣺���ڢ٣�max{x1��x2}��a?x1��a��x2��a���ʢٴ���
���ڢڣ�max{x1��x2}��a?x1��a��x2��a���ʢ���ȷ��
���ڢۣ��躯��f��x����g��x���Ĺ���������ΪD����x��D��f��x����g��x�����������[f��x��]min��[g��x��]max���ʢ���ȷ��
���ڢܣ�������f��x��=min{|x|��|x+t|}��ͼ�����ֱ��x=-
�Գƣ���ͼ���£�
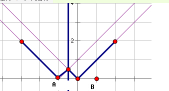
ͼ���е��ұ���y=|x|�������y=|x+t|����Ϊ����f��x��=min{|x|��|x+t|}��ͼ�����ֱ��x=-
�Գƣ�
����y=|x|��y=|x+t|�Ľ��������Ϊx=-
����֪AB���е������Ϊx=-
��
����A��-1��0�������У�t=1���ʢ���ȷ��
�ʴ�Ϊ���ڢۢܣ�
���ڢڣ�max{x1��x2}��a?x1��a��x2��a���ʢ���ȷ��
���ڢۣ��躯��f��x����g��x���Ĺ���������ΪD����x��D��f��x����g��x�����������[f��x��]min��[g��x��]max���ʢ���ȷ��
���ڢܣ�������f��x��=min{|x|��|x+t|}��ͼ�����ֱ��x=-
| 1 |
| 2 |

ͼ���е��ұ���y=|x|�������y=|x+t|����Ϊ����f��x��=min{|x|��|x+t|}��ͼ�����ֱ��x=-
| 1 |
| 2 |
����y=|x|��y=|x+t|�Ľ��������Ϊx=-
| 1 |
| 2 |
| 1 |
| 2 |
����A��-1��0�������У�t=1���ʢ���ȷ��
�ʴ�Ϊ���ڢۢܣ�
���������⿼�麯������ֵ���⣬���ؿ������������뺯���ĶԳ��ԣ���ͼ�ǹؼ���Ҳ���ѵ㣬�������⣮

��ϰ��ϵ�д�
�����Ŀ
�輯��M={x|
��0}��N={x|log2��x+1����2}����M��N=��������
| x+1 |
| x-2 |
| A����-1��2] |
| B��[-1��2�� |
| C����-1��2�� |
| D��[-1��2] |
��������ABCD-A1B1C1D1�У�AB=2��E����CD���е㣬������A1-BB1E�����Ϊ��������
A��
| ||
B��
| ||
C��
| ||
D��
|