题目内容
已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)若![]() 满足
满足![]() 恒成立,则称
恒成立,则称![]() 的一个“上界函数”,如果
的一个“上界函数”,如果
函数![]() 为
为![]() (
(![]() 为实数)的一个“上界函数”,求
为实数)的一个“上界函数”,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,讨论
时,讨论![]() 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.
解:(Ⅰ)当![]() 时,
时,![]() ,代入
,代入![]() 得
得![]() ,所以
,所以![]() ,
,
![]() ,由切线方程知
,由切线方程知![]() ,所以
,所以![]() ,故
,故![]() .
.
(Ⅱ)![]() 恒成立,即
恒成立,即![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 为增函数;
为增函数;
![]() 的最小值为
的最小值为![]() ,故
,故![]() .
.
(Ⅲ)由已知![]() ,
,![]()
 ,
,
又![]() ,由
,由![]() 得,
得,![]() ,
,![]() .
.
(1)当![]() 时,得
时,得![]() ,
,![]() ,
,![]() 在(0,2)为增函数,无极值点;
在(0,2)为增函数,无极值点;
(2)当 且
且![]() 时,得
时,得![]() 且
且![]() ,
,![]() 有2个极值点;
有2个极值点;
(3)当 或
或 时,得
时,得![]() 或
或![]() 时,
时,![]() 有1个极值点;
有1个极值点;
综上,当![]() 时,函数
时,函数![]() 在(0,2)无极值点;当
在(0,2)无极值点;当![]() 或
或![]() 时,
时,![]() 有1个极值点;当
有1个极值点;当![]() 且
且![]() 时,
时,![]() 有2个极值点.
有2个极值点.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
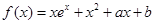 在点
在点 处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+
处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+ )均有
)均有 恒成立.
恒成立.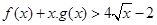 .
.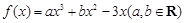 在点
在点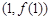 处的切线方程为
处的切线方程为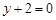 .
.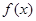 的解析式;
的解析式;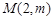 可以作出曲线
可以作出曲线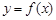 的三条切线,求实数
的三条切线,求实数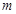 的取值范围.
的取值范围.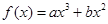 在点
在点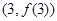 处的切线方程为
处的切线方程为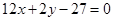 ,且对任意的
,且对任意的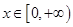 ,
,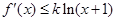 恒成立.
恒成立.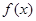 的解析式;
的解析式;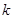 的最小值;
的最小值;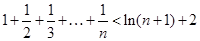 (
(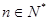 ).
).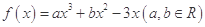 在点
在点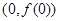 处的切线与直线
处的切线与直线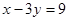 垂直.
垂直.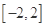 上任意两个自变量的值
上任意两个自变量的值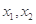 都有
都有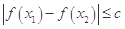 ,求实数
,求实数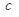 的最小值;
的最小值;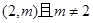 可作曲线
可作曲线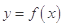 的三条切线,求实数
的三条切线,求实数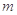 的取值范围.
的取值范围. 在点
在点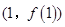 处的切线方程为
处的切线方程为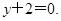
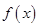 的解析式;
的解析式;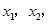 都有
都有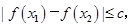 求实数c的最小值.
求实数c的最小值.