题目内容
1.已知⊙O是边长为2的正方形ABCD的内切圆,P是⊙O上任意一点,则AP+$\sqrt{2}$BP的最小值为$\sqrt{5}$.分析 连接OA、OE、OB,OB交⊙O于点P,此时BP+$\frac{\sqrt{2}}{2}$AP的值最小;由⊙O是正方形ABCD的内切圆得出BE=OE=OP=$\frac{1}{2}$BC=1,OE⊥BC,OA⊥OB,OB=OA=$\sqrt{2}$BE=$\sqrt{2}$,得出BP,由勾股定理求出AP,即可得出结果.
解答 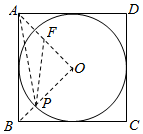 解:如图所示:
解:如图所示:
取AO的中点F
所以$\frac{PO}{FO}$=$\frac{AO}{PO}$=$\sqrt{2}$,又∠POF=∠AOP
所以△POF~△AOP
所以PF=$\frac{\sqrt{2}}{2}$AP,
所以F,P,B三点共线时BP+$\frac{\sqrt{2}}{2}$AP取最小值为$\frac{\sqrt{10}}{2}$.
所以$\sqrt{2}$(BP+$\frac{\sqrt{2}}{2}$AP)=$\sqrt{2}$•$\frac{\sqrt{10}}{2}$=$\sqrt{5}$
点评 本题考查了正方形的性质、正方形的内切圆的性质、勾股定理、等腰直角三角形的性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
12.今年是我校成立111周年的一年,那么十进制的111化为二进制是( )
| A. | 1 101 101 | B. | 11 011 011 | C. | 1 101 111 | D. | 1 011 100 |
13.根据如图所示的算法语句,可知输出的结果S是( )


| A. | 11 | B. | 9 | C. | 7 | D. | 5 |
11.已知$cos({α+\frac{π}{6}})=\frac{1}{3}$,$α∈[{0,\frac{π}{2}}]$,那么cosα等于( )
| A. | $\frac{2\sqrt{2}-\sqrt{3}}{6}$ | B. | $\frac{2\sqrt{2}+\sqrt{3}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{2}}{6}$ | D. | $\frac{2\sqrt{3}+\sqrt{2}}{6}$ |
 已知一个三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2\sqrt{3}}{3}$.外接球半径为$\sqrt{5}$.
已知一个三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2\sqrt{3}}{3}$.外接球半径为$\sqrt{5}$.
 如图,在正方体A1B1C1D1-ABCD中,
如图,在正方体A1B1C1D1-ABCD中,