题目内容
17.在平面直角坐标系xOy中,圆C的极坐标方程为ρ=4,经过点P(1,2)的直线l的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{3}t}\\{y=2+t}\end{array}\right.$(t为参数).(1)写出圆C的标准方程和直线l的普通方程;
(2)设直线l与圆C相交于A,B两点,求$\frac{1}{|PA|}$+$\frac{1}{|PB|}$的值.
分析 (1)利用ρ2=x2+y2=4可得⊙C的标准方程4,直线l的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{3}t}\\{y=2+t}\end{array}\right.$(t为参数),消去t可得直线l的普通方程.
(2)直线l的标准参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=2+\frac{1}{2}t}\end{array}\right.$(t为参数),代入⊙C的方程可得:t2+(2+$\sqrt{3}$)t+1=0,利用根与系数的关系及其参数的意义可得$\frac{1}{|PA|}$+$\frac{1}{|PB|}$=$\frac{1}{|{t}_{1}|}+\frac{1}{|{t}_{2}|}$=-$\frac{{t}_{1}+{t}_{2}}{{t}_{1}{t}_{2}}$.
解答 解:(1)由ρ=4可得⊙C的标准方程:x2+y2=4,
直线l的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{3}t}\\{y=2+t}\end{array}\right.$(t为参数),消去t可得:直线l的普通方程:$x-\sqrt{3}y$+2$\sqrt{3}$-1=0.
(2)直线l的标准参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=2+\frac{1}{2}t}\end{array}\right.$(t为参数),代入⊙C的方程可得:t2+(2+$\sqrt{3}$)t+1=0,
∴t1+t2=-(2+$\sqrt{3}$),t1t2=1.
∴$\frac{1}{|PA|}$+$\frac{1}{|PB|}$=$\frac{1}{|{t}_{1}|}+\frac{1}{|{t}_{2}|}$=-$\frac{{t}_{1}+{t}_{2}}{{t}_{1}{t}_{2}}$=$2+\sqrt{3}$.
点评 本题考查了极坐标化为直角坐标方程、直线与圆的位置关系、直线参数方程的应用,考查了数形结合方法、推理能力与计算能力,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | g(x)的最大值为2 | B. | g(x)在[0,$\frac{π}{2}$]上是增函数 | ||
| C. | 函数g(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | 函数g(x)的图象关于点($\frac{π}{12}$,0)对称 |
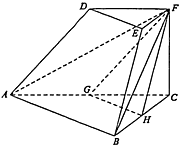 如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.