题目内容
某同学参加某高校自主招生3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为
，第二、第三门课程取得优秀成绩的概率分别为p，q(p＜q)，且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为
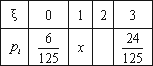
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p，q的值；
(Ⅱ)求数学期望Eξ．
答案：
解析：
解析：
|
解：用 由题意得 (Ⅰ)该生至少有一门课程取得优秀成绩的概率为 (Ⅱ) 及 (2)
∴ ∴该生取得优秀成绩的课程门数的期望为 |
表示“该生第
门课程取得优秀成绩”，
得
．
练习册系列答案
走进文言文系列答案
相关题目
某同学参加某高校自主招生3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为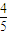
，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为
（Ⅰ）求该生至少有1门课程取得优秀成绩的概率及求p，q的值；
（Ⅱ） 求数学期望Eξ．
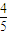，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为| ξ | 1 | 2 | 3 | |
| pi | 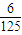 | x | y |  |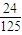
（Ⅱ） 求数学期望Eξ．
某同学参加某高校自主招生3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为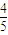
，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为
（Ⅰ）求该生至少有1门课程取得优秀成绩的概率及求p，q的值；
（Ⅱ） 求数学期望Eξ．
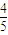，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为| ξ | 1 | 2 | 3 | |
| pi | 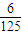 | x | y |  |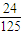
（Ⅱ） 求数学期望Eξ．