��Ŀ����
ijͬѧ�μ�ij��У��������3�ſγ̵Ŀ��ԣ������ͬѧ��һ�ſγ�ȡ������ɼ��ĸ���Ϊ
���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���������������1�ſγ�ȡ������ɼ��ĸ��ʼ���p��q��ֵ��
���� ����ѧ����E�Σ�
| 4 |
| 5 |
| �� | 0 | 1 | 2 | 3 | ||||
| pi |
|
x | y |
|
���� ����ѧ����E�Σ�
������������Ai��ʾ��������i�ſγ�ȡ������ɼ�����i=1��2��3���������P(A1)=
��P(
1
2
3)=
���ɴ����������������һ�ſγ�ȡ������ɼ��ĸ��ʣ��Ӷ��ܹ����p��q��ֵ��
����������֪�εĿ���ȡֵΪ0��1��2��3���ֱ��������ʣ��ɴ��ܹ������ѧ����E�Σ�
| 4 |
| 5 |
. |
| A |
. |
| A |
. |
| A |
| 6 |
| 125 |
����������֪�εĿ���ȡֵΪ0��1��2��3���ֱ��������ʣ��ɴ��ܹ������ѧ����E�Σ�
����⣺��Ai��ʾ��������i�ſγ�ȡ������ɼ�����i=1��2��3��
�������P(A1)=
��P(
1
2
3)=
������������һ�ſγ�ȡ������ɼ��ĸ���ΪP=1-P(
1
2
3)=1-
=
P(
)=(1-P(A1))(1-P(A2))(1-P(A3))=
(1-p)(1-q)=
��P(A1A2A3)=P(A1)P(A2)P(A3)=
pq=
��p=
��q=
��
����������֪�εĿ���ȡֵΪ0��1��2��3��
P����=0��=
��
P(��=1)=
��
��
+
��
��
+
��
��
=
��P(��=2)=
��
��
+
��
��
+
��
��
=
��
P����=3��=1-
-
-
=
��
��E(��)=0��
+1��
+2��
+3��
=
��
�����ȡ������ɼ��Ŀγ�����������Ϊ
��
�������P(A1)=
| 4 |
| 5 |
. |
| A |
. |
| A |
. |
| A |
| 6 |
| 125 |
������������һ�ſγ�ȡ������ɼ��ĸ���ΪP=1-P(
. |
| A |
. |
| A |
. |
| A |
| 6 |
| 125 |
| 119 |
| 125 |
P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
| 1 |
| 5 |
| 6 |
| 125 |
��P(A1A2A3)=P(A1)P(A2)P(A3)=
| 4 |
| 5 |
| 24 |
| 125 |
| 2 |
| 5 |
| 3 |
| 5 |
����������֪�εĿ���ȡֵΪ0��1��2��3��
P����=0��=
| 6 |
| 125 |
P(��=1)=
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 37 |
| 125 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 58 |
| 125 |
P����=3��=1-
| 6 |
| 125 |
| 37 |
| 125 |
| 58 |
| 125 |
| 24 |
| 125 |
| �� | 0 | 1 | 2 | 3 | ||||||||
| pi |
|
|
|
|
| 6 |
| 125 |
| 37 |
| 125 |
| 58 |
| 125 |
| 24 |
| 125 |
| 9 |
| 5 |
�����ȡ������ɼ��Ŀγ�����������Ϊ
| 9 |
| 5 |
���������⿼����ɢ��������ĸ��ʷֲ��к���ѧ������������߿��ıؿ�����֮һ������ʱҪ�������⣬ע���������֪ʶ����֪ʶ��������ã�

��ϰ��ϵ�д�
 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
�����Ŀ
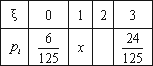
ijͬѧ�μ�ij��У��������3�ſγ̵Ŀ��ԣ������ͬѧ��һ�ſγ�ȡ������ɼ��ĸ���Ϊ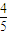 ���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���������������1�ſγ�ȡ������ɼ��ĸ��ʼ���p��q��ֵ��
���� ����ѧ����E�Σ�
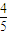 ���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ| �� | 1 | 2 | 3 | |
| pi | 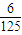 | x | y | 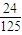 |
���� ����ѧ����E�Σ�
ijͬѧ�μ�ij��У��������3�ſγ̵Ŀ��ԣ������ͬѧ��һ�ſγ�ȡ������ɼ��ĸ���Ϊ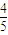 ���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���������������1�ſγ�ȡ������ɼ��ĸ��ʼ���p��q��ֵ��
���� ����ѧ����E�Σ�
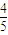 ���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ
���ڶ��������ſγ�ȡ������ɼ��ĸ��ʷֱ�Ϊp��q��p��q�����Ҳ�ͬ�γ��Ƿ�ȡ������ɼ���������Ǧ�Ϊ����ȡ������ɼ��Ŀγ�������ֲ���Ϊ| �� | 1 | 2 | 3 | |
| pi | 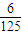 | x | y | 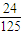 |
���� ����ѧ����E�Σ�