题目内容
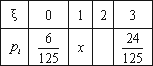
某同学参加某高校自主招生3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为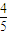 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为| ξ | 1 | 2 | 3 | |
| pi | 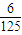 | x | y | 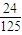 |
(Ⅱ) 求数学期望Eξ.
【答案】分析:(Ⅰ)用Ai表示“该生第i门课程取得优秀成绩”,i=1,2,3.由题意得 ,
, ,由此能求出该生至少有一门课程取得优秀成绩的概率.从而能够求出p,q的值.
,由此能求出该生至少有一门课程取得优秀成绩的概率.从而能够求出p,q的值.
(Ⅱ)由题设知ξ的可能取值为0,1,2,3,分别求出其概率,由此能够求出数学期望Eξ.
解答:解:用Ai表示“该生第i门课程取得优秀成绩”,i=1,2,3.
由题意得 ,
,
(Ⅰ)该生至少有一门课程取得优秀成绩的概率为

及 得
得 .
.
(Ⅱ)由题设知ξ的可能取值为0,1,2,3,
P(ξ=0)= ,
,
 ,
, ,
,
P(ξ=3)=1- -
- -
- =
= .
.
∴ .
.
∴该生取得优秀成绩的课程门数的期望为 .
.
点评:本题考查离散随机变量的概率分布列和数学期望,是历年高考的必考题型之一.解题时要认真审题,注意排列组合知识和概率知识的灵活运用.
 ,
, ,由此能求出该生至少有一门课程取得优秀成绩的概率.从而能够求出p,q的值.
,由此能求出该生至少有一门课程取得优秀成绩的概率.从而能够求出p,q的值.(Ⅱ)由题设知ξ的可能取值为0,1,2,3,分别求出其概率,由此能够求出数学期望Eξ.
解答:解:用Ai表示“该生第i门课程取得优秀成绩”,i=1,2,3.
由题意得
 ,
,
(Ⅰ)该生至少有一门课程取得优秀成绩的概率为


及
 得
得 .
.(Ⅱ)由题设知ξ的可能取值为0,1,2,3,
P(ξ=0)=
 ,
, ,
, ,
,P(ξ=3)=1-
 -
- -
- =
= .
.| ξ | 1 | 2 | 3 | |
| pi |  |  |  |  |
 .
.∴该生取得优秀成绩的课程门数的期望为
 .
.点评:本题考查离散随机变量的概率分布列和数学期望,是历年高考的必考题型之一.解题时要认真审题,注意排列组合知识和概率知识的灵活运用.

练习册系列答案
相关题目
某同学参加某高校自主招生3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为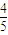 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ) 求数学期望Eξ.
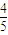 ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为| ξ | 1 | 2 | 3 | |
| pi | 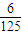 | x | y | 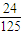 |
(Ⅱ) 求数学期望Eξ.