题目内容
已知 t=
(u>1),且关于t的不等式t2-8t+m+18<0有解,则实数m的取值范围是( )
| -u2+7u-7 |
| u-1 |
| A、(-∞,-3) |
| B、(-3,+∞) |
| C、(3,+∞) |
| D、(-∞,3) |
考点:基本不等式
专题:不等式的解法及应用
分析:u>1,可得u-1>0.t=
=-[(u-1)+
]+5,利用基本不等式的性质可得t∈(1,3].
不等式t2-8t+m+18<0,化为m<-t2+8t-18,因此关于t的不等式t2-8t+m+18<0有解?m<(-t2+8t-18)max.利用二次函数的单调性即可得出.
| -u2+7u-7 |
| u-1 |
| 1 |
| u-1 |
不等式t2-8t+m+18<0,化为m<-t2+8t-18,因此关于t的不等式t2-8t+m+18<0有解?m<(-t2+8t-18)max.利用二次函数的单调性即可得出.
解答:
解:∵u>1,∴u-1>0.
∴t=
=
=-[(u-1)+
]+5≤-2
+5=3,当且仅当u=2时取等号.
∴t∈(1,3].
∵不等式t2-8t+m+18<0,化为m<-t2+8t-18,
∴关于t的不等式t2-8t+m+18<0有解?m<(-t2+8t-18)max.
令f(t)=-t2+8t-18=-(t-4)2-2≤f(3)=-3.
因此m<-3.
故选:A.
∴t=
| -u2+7u-7 |
| u-1 |
| -(u-1)2+5(u-1)-1 |
| u-1 |
| 1 |
| u-1 |
(u-1)•
|
∴t∈(1,3].
∵不等式t2-8t+m+18<0,化为m<-t2+8t-18,
∴关于t的不等式t2-8t+m+18<0有解?m<(-t2+8t-18)max.
令f(t)=-t2+8t-18=-(t-4)2-2≤f(3)=-3.
因此m<-3.
故选:A.
点评:本题考查了基本不等式的性质、二次函数的单调性、恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
若不等式x2+kx+1<0的解集为空集,则k的取值范围是( )
| A、[-2,2] |
| B、(-∞,-2]∪[2,+∞) |
| C、(-2,2) |
| D、(-∞,-2)∪(2,+∞) |
在△ABC中,已知A=60°,a=
,b=
,则B等于( )
| 3 |
| 2 |
| A、45°或135° | B、60° |
| C、45° | D、135° |
函数y=logax (0<a<1)的图象大致是( )
A、 |
B、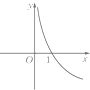 |
C、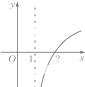 |
D、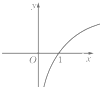 |
已知
是实数,则“
”是“
”的( )
| 1 |
| 2 |
| 1 |
| 2x |
| 7 |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
下列函数在区间(-∞,0)上为增函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=-x2-2x-1 | ||
| D、y=1+x2 |
f(x)是定义在(-1,1)上的奇函数且单调递减,若f(2-a)+f(4-a2)<0,则a的取值范围是( )
A、(
| ||
B、(-∞,
| ||
C、(
| ||
D、(-∞,
|
已知等差数列{an}中,a2+a4=6,则前5项和S5为( )
| A、5 | B、6 | C、15 | D、30 |